Tentamen i MAN011 Aritmetik och Algebra del 1, 5p, 98 04 08.

1.

(a)

Formulera och bevisa en sats om eventuella rationella nollställen till ett polynom med heltalskoefficienter.

(b)

Har polynomet z³+5z²/2-z-1 något rationellt nollställe?

2.

Bevisa kinesiska restsatsen. (Fallet med två ekvationer räcker.)

3.

(a)

Visa att en delgrupp till en cyklisk grupp är cyklisk.

(b)

Visa att 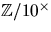$\mathbb Z/10^{\times}$ är cyklisk.

4.

Bestäm alla positiva heltal x och y så att

33x+21y=444.

5.

På hur många sätt kan man växla tjugotre kronor i enkronor, femkronor och tior?

6.

Ekvationen

z³-(4+i)z²+(4+6i)z+2-4i=0

har roten 1+i. Lös ekvationen.

7.

Låt p(n)=n⁵+10n⁴+35n³+50n²+24n.

(a)

Visa att 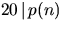$20\,\vert\,p(n)$ för alla heltal n.

(b)

Bestäm det största heltalet m så att 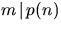$m\,\vert\,p(n)$ för alla heltal n.

8.

Hur många delgrupper av ordning 2, 3, 5 och 10 har diedergruppen D₂₅?