Tentamen i MAN011 Aritmetik och algebra, del 1,
99 01 04, kl 8.45-13.45
- 1.
- Formulera och bevisa triangelolikheten för komplexa tal.
- 2.
- (a)
- Vad menas med, enligt definitionen,
en största gemensam
delare till två polynom
f(x) och g(x) i
![$\mathbb Q[x]$](img1.gif) ?
?
- (b)
- Visa två polynom i f(x) och g(x) i
![$\mathbb Q[x]$](img1.gif) har en
största gemensam delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x) för några polynom a(x) och b(x) i
har en
största gemensam delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x) för några polynom a(x) och b(x) i
![$\mathbb Q[x]$](img1.gif) .
.
- 3.
- Formulera och bevisa Lagranges sats.
- 4.
- Visa att
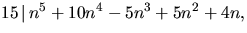 när n är ett heltal.
när n är ett heltal.
- 5.
- Talföljden an definieras av
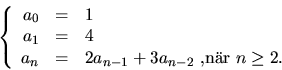
Visa att
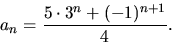
- 6.
- Den komplexa tredjegradsekvationen
z3-(5+i)z2+(11+2i)z+9i-7=0
har lösningen z=-i. Bestäm samtliga lösningar.
- 7.
- Hur många delgrupper av ordning
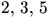 och 7 har D15?
Motivera noggrant!
och 7 har D15?
Motivera noggrant!
- 8.
- Hur många femsiffriga tal har ett udda antal 1:or?
![$\mathbb Q[x]$](img1.gif) ?
?
![$\mathbb Q[x]$](img1.gif) har en
största gemensam delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x) för några polynom a(x) och b(x) i
har en
största gemensam delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x) för några polynom a(x) och b(x) i
![$\mathbb Q[x]$](img1.gif) .
. 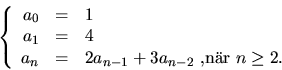
![]()