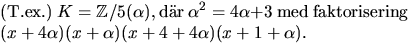Lösningar till tentamen i MAN011 Aritmetik och
algebra, del 2, 98 01 17.
- 4.
- För att visa att ringen är en kropp gäller det att visa att
![$p(x)=x^{2}+3x+1\in \mathbb Q[x]$](img1.gif) är irreducibelt. Eftersom polynomet
är av grad 2 räcker det att visa att det saknar faktor av grad 1.
Enligt faktorsatsen är detta det samma som att visa att p(x) saknar
rationellt nollställe. De möjliga rationella nollställena är
är irreducibelt. Eftersom polynomet
är av grad 2 räcker det att visa att det saknar faktor av grad 1.
Enligt faktorsatsen är detta det samma som att visa att p(x) saknar
rationellt nollställe. De möjliga rationella nollställena är 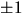 och inget duger. Därmed är p(x) irreducibelt och
och inget duger. Därmed är p(x) irreducibelt och 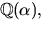 där
där 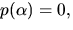 en kropp.
För att invertera
en kropp.
För att invertera 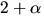 bestämmer vi en största gemensam delare
med
bestämmer vi en största gemensam delare
med 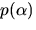 med hjälp av Euklides algoritm:
med hjälp av Euklides algoritm:
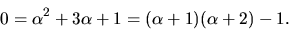
Detta ger 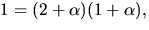 så
så 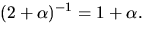
Svar: 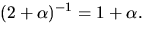
- 5.
- Vi bestämmer först egenvärden till A genom att bestämma värden på
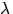 så att
så att 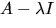 har rang
har rang 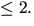 Vi gör
radoperationer:
Vi gör
radoperationer:
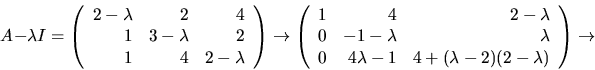
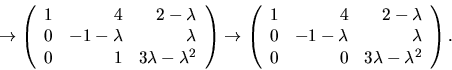
Vi ser att rangen är 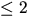 om och endast om
om och endast om
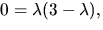 eller
eller 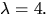 Egenvärdena är alltså
Egenvärdena är alltså
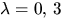 och 4.
och 4.
Vi bestämmer en egenvektor hörande till vart och ett av egenvärdena
och utnyttjar räkningen ovan:
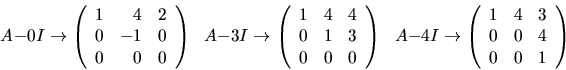
Vi har (t.ex.) egenvektorerna 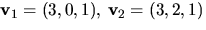 och
och 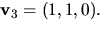 Om
Om 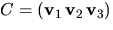 har vi att AC=CD, där
har vi att AC=CD, där
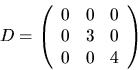
Eftersom egenvektorerna hör till olika egenvärden är de linjärt
oberoende och C har därför rang 3 och är därmed inverterbar.
Svar: 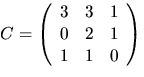 och
och
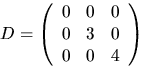
- 6.
- Eftersom
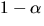 är ett nollställe till f(x) vet vi att
är ett nollställe till f(x) vet vi att
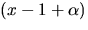 delar f(x). Vi utför divisionen och får:
delar f(x). Vi utför divisionen och får:
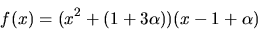
Eftersom 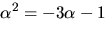 har vi
har vi
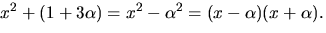 Detta ger
Detta ger
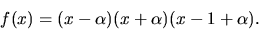
Svar: 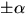 och
och 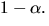
- 7.
- Vi sätter
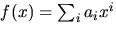 och bestämmer först ett uttryck
för f(x). Om vi sätter p(x)=1-3x/2+x2/2 har vi att
och bestämmer först ett uttryck
för f(x). Om vi sätter p(x)=1-3x/2+x2/2 har vi att
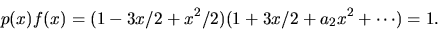
Vi har alltså f(x)=2/(2-3x+x2)=2/(1-x)(2-x). Multipicerar vi f(x) med
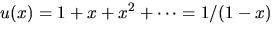 får vi en ny potensserie vars
koefficient framför xn är den sökta summan. Ansättning för
partialbråksuppdelning ger
får vi en ny potensserie vars
koefficient framför xn är den sökta summan. Ansättning för
partialbråksuppdelning ger
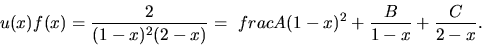
Handpåläggning ger 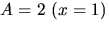 och
och 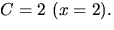 Sätter vi x=0
får vi 1=A+B+C/2=3+B, så B=-2. Vi får
Sätter vi x=0
får vi 1=A+B+C/2=3+B, så B=-2. Vi får
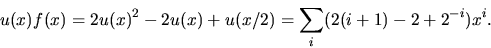
Svar: 2n+2-n.
- 8.
- Vi underöker om
![$p(x)=x^{4}+3x^{2}+4\in \mathbb Z/5[x]$](img41.gif) faktoriserar. Eftersom
faktoriserar. Eftersom 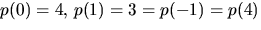 och
p(2)=2=p(-2)=p(3), saknar polynomet nollställe och, enligt
Faktorsatsen, därmed faktor av grad 1 (och följdaktligen faktor av
grad 3.) Vi undersöker om p(x) är produkt av två polynom av grad
2 genom att ansätta p(x)=(x2+ax+b)(x2+cx+d), där
och
p(2)=2=p(-2)=p(3), saknar polynomet nollställe och, enligt
Faktorsatsen, därmed faktor av grad 1 (och följdaktligen faktor av
grad 3.) Vi undersöker om p(x) är produkt av två polynom av grad
2 genom att ansätta p(x)=(x2+ax+b)(x2+cx+d), där 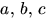 och
och 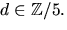 Utveckling ger ekvationssystemet
Utveckling ger ekvationssystemet
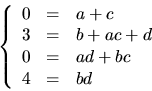
Den sista ekvationen ger 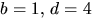 eller b=2=d eller motsvarande
där b och d byter plats. Sista alternativet ger ac=2 i andra
ekvationen. Tillsammans med den första ger detta a2=4. Eftersom
eller b=2=d eller motsvarande
där b och d byter plats. Sista alternativet ger ac=2 i andra
ekvationen. Tillsammans med den första ger detta a2=4. Eftersom
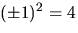 har vi lösningen
har vi lösningen 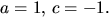
Vi får
p(x)=(x2+x+2)(x2+4x+2)
där de två faktorerna är irreducibla.
Vi har alltså kroppen 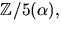 där
där
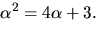 Vi faktoriserar x2+x+2 med Faktorsatsen
och får
Vi faktoriserar x2+x+2 med Faktorsatsen
och får

Polynomet p(x) har alltså nollställena
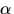 och
och 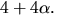 Eftersom p(-x)=p(x) är också
Eftersom p(-x)=p(x) är också 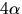 och
och
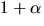 nollställen till p(x). Enligt faktorsatsen har vi
faktoriseringen
nollställen till p(x). Enligt faktorsatsen har vi
faktoriseringen
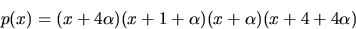
Svar: 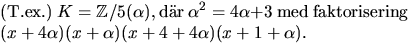
![]()
![]()
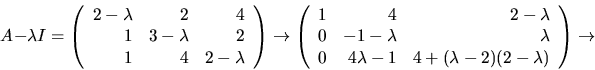
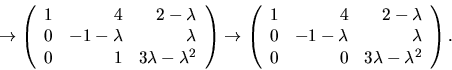
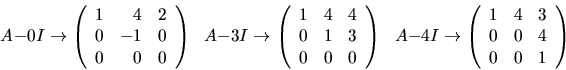
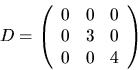
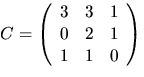 och
och
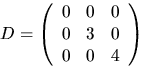
![]()
![]()
![]() och
och ![]()
![]()
![]()
![]()
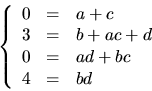
![]() där
där
![]() Vi faktoriserar x2+x+2 med Faktorsatsen
och får
Vi faktoriserar x2+x+2 med Faktorsatsen
och får
![]()
![]()