Lösningar till tentamen i Aritmetik och algebra,
del 2, 98 04 04
- 4.
- Vi undersöker om A är inverterbar:
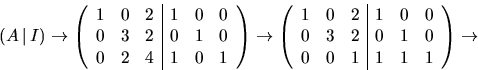
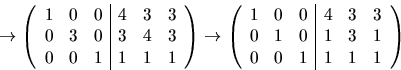
Vi ser att A är inverterbar med den högra halvan som invers. Detta
ger att X=A-1B, dvs
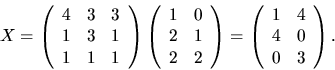
Svar: 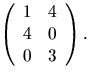
- 5.
- Det gäller att visa att
![$p(x)=x^{4}-3x+4\in \mathbb Q[x]$](img5.gif) är
irreducibelt. Vi undersöker först om det har en faktor av grad 1.
Enligt Faktorsatsen motsvarar en sådan ett rationellt nollställe. De
möjliga rationella nollställena är
är
irreducibelt. Vi undersöker först om det har en faktor av grad 1.
Enligt Faktorsatsen motsvarar en sådan ett rationellt nollställe. De
möjliga rationella nollställena är 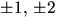 och
och 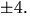 Vi ser genast att negativa värden är uteslutna och att p(4)>0. Vi
har också p(1)=2 och p(2)=14. Polynomet saknar därmed faktor av
grad 1 och följdaktligen även faktor av grad 3. Vi undersöker om
p(x) är produkt av två polynom av grad 2 genom att ansätta
p(x)=(x2+ax+b)(x2+cx+d). Eftersom p(x) är primitivt kan vi
förutsätta att
Vi ser genast att negativa värden är uteslutna och att p(4)>0. Vi
har också p(1)=2 och p(2)=14. Polynomet saknar därmed faktor av
grad 1 och följdaktligen även faktor av grad 3. Vi undersöker om
p(x) är produkt av två polynom av grad 2 genom att ansätta
p(x)=(x2+ax+b)(x2+cx+d). Eftersom p(x) är primitivt kan vi
förutsätta att 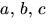 och d är heltal. Vi får ekvationssystemet
och d är heltal. Vi får ekvationssystemet
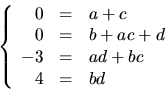
Den nedersta ekvationen ger 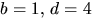 eller
eller 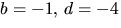 eller
eller
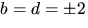 eller motsvarande där b och d byter plats. Om b=d
strider första och tredje ekvationerna mot varandra. Fallet
eller motsvarande där b och d byter plats. Om b=d
strider första och tredje ekvationerna mot varandra. Fallet
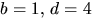 ger -3=4a+c i tredje ekvationen. Tillsammans med första
ekvationen ger detta
ger -3=4a+c i tredje ekvationen. Tillsammans med första
ekvationen ger detta 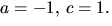 Men detta strider mot andra
ekvationen. Fallet
Men detta strider mot andra
ekvationen. Fallet 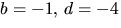 ger -3=-4a-c i tredje
ekvationen. Tillsammans med den första ger detta
ger -3=-4a-c i tredje
ekvationen. Tillsammans med den första ger detta 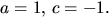 Men
detta stridet mot den andra ekvationen. Ekvationssystemet saknar
lösning och därmed saknar p(x) faktor av grad 2. Alltså är
polynomet irreducibelt och
Men
detta stridet mot den andra ekvationen. Ekvationssystemet saknar
lösning och därmed saknar p(x) faktor av grad 2. Alltså är
polynomet irreducibelt och 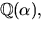 där
där 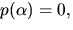 är
en kropp.
är
en kropp.
Vi inverterar 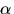 geom att söka en största gemensam delare till
polynomen
geom att söka en största gemensam delare till
polynomen 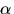 och
och 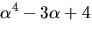 med Euklides algoritm:
med Euklides algoritm:
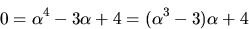
Detta ger 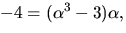 så
så 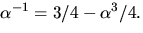
Svar: 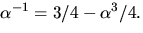
- 6.
- Vi undersöker om
![$f(x)=x^{4}+3x^{2}+3\in\mathbb Z/5[x]$](img22.gif) faktoriserar.
Eftersom
faktoriserar.
Eftersom 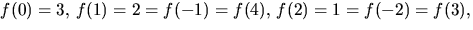 saknar
polynomet faktor av grad 1 enligt Faktorsasten och därmed även
faktor av grad 3. Vi undersöker om polynomet är produkt av två
polynom av grad 2 genom att ansätta f(x)=(x2+ax+b)(x2+cx+d),
där
saknar
polynomet faktor av grad 1 enligt Faktorsasten och därmed även
faktor av grad 3. Vi undersöker om polynomet är produkt av två
polynom av grad 2 genom att ansätta f(x)=(x2+ax+b)(x2+cx+d),
där 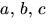 och
och 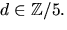 Detta ger ekvationssystemet
Detta ger ekvationssystemet
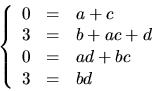
Den nedersta ekvationen ger 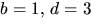 eller
eller 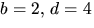 eller
motsvarande där b och d byter plats. De båda alternativen ger
0=3a+c respektive 0=4a+2c i tredje ekvationen. Tillsammans med den
första ekvationen ger detta a=0=c i båda fallen. Detta strider mot
den andra ekvationen.
eller
motsvarande där b och d byter plats. De båda alternativen ger
0=3a+c respektive 0=4a+2c i tredje ekvationen. Tillsammans med den
första ekvationen ger detta a=0=c i båda fallen. Detta strider mot
den andra ekvationen.
Eftersom f(x) är irreducibelt har vi kroppen 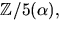 där
där 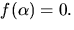 Vi ser att
Vi ser att 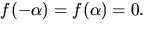 Eftersom
Eftersom
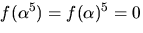 har vi också nollställena
har vi också nollställena 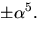 Vi beräknar
Vi beräknar 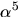 genom att utnyttja att
genom att utnyttja att
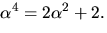 Detta ger
Detta ger
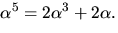 Faktorsatsen ger nu
Faktorsatsen ger nu
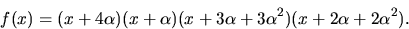
Svar: 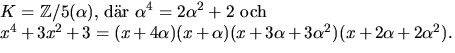
- 7.
- Vi skriver om f och g med hjälp av
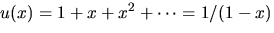 och utnyttjar att
och utnyttjar att
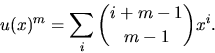
Vi har
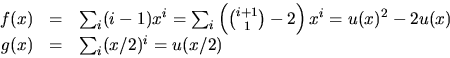
och får
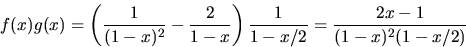
Vi gör en partialbråksuppdelning och ansätter
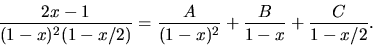
Konstanterna A och C bestäms med handpåläggning till 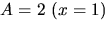 och
och 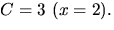 Vi sätter x=0 och får -1=2+B+3, så B=-6.
Vi får
Vi sätter x=0 och får -1=2+B+3, så B=-6.
Vi får
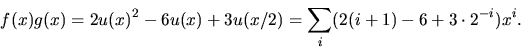
Svar: 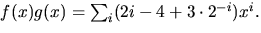
- 8.
- De gemensamma nollställena till polynomen är nollställen till en
största gemensam delare till dem. Vi bestämmer därför en sådan
med Euklides algoritm:
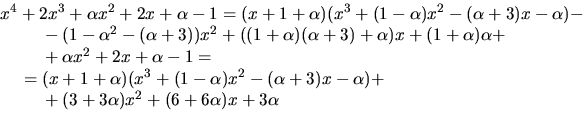
Vi förenklar resten genom att multiplicera med 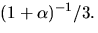 Vi bestämmer
Vi bestämmer 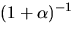 med Euklides algoritm:
med Euklides algoritm:
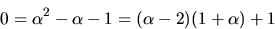
Detta ger 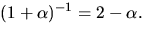 Den förenklade resten blir
Den förenklade resten blir
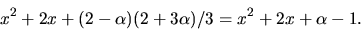
Vi fortsätter beräkningen av en största gemensam delare:
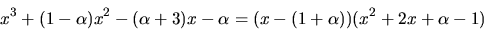
Eftersom divisionen gick jämnt ut är 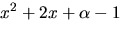 en störtsta
gemensam delare. Vi bestämmer dess nollställen:
en störtsta
gemensam delare. Vi bestämmer dess nollställen: 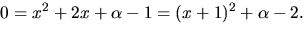 Vi sätter
Vi sätter 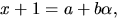 där
där 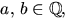 och ska lösa
och ska lösa 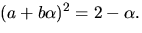 Utveckling ger
ekvationssystemet
Utveckling ger
ekvationssystemet
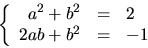
Den nedre ekvationen multipiceras med 2 och läggs till den
övre. Detta ger 0=a2+4ab+3b2=(a+2b)2-b2=(a+b)(a+3b), med
lösningen b=-a och a=-3b. Det sista alternativet ger b2=1/5,
som saknar rationell lösning, i den första ekvationen. Det första
alternativet ger 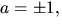 som ger lösningarna
som ger lösningarna 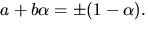 Eftersom
Eftersom 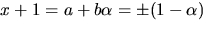 får vi
nollställena
får vi
nollställena 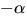 och
och 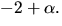
Svar: 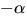 och
och 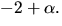
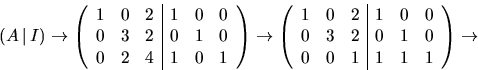
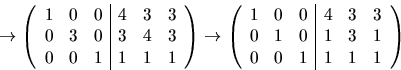
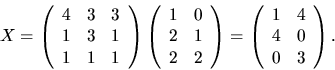
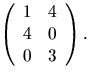
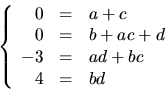
![]() geom att söka en största gemensam delare till
polynomen
geom att söka en största gemensam delare till
polynomen ![]() och
och ![]() med Euklides algoritm:
med Euklides algoritm:
![]()
![]()
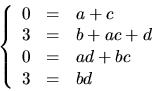
![]() där
där ![]() Vi ser att
Vi ser att ![]() Eftersom
Eftersom
![]() har vi också nollställena
har vi också nollställena ![]() Vi beräknar
Vi beräknar ![]() genom att utnyttja att
genom att utnyttja att
![]() Detta ger
Detta ger
![]() Faktorsatsen ger nu
Faktorsatsen ger nu
![]()
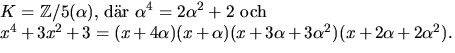
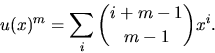
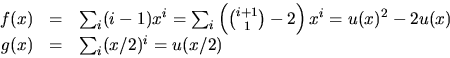
![]()
![]()
![]()
![]()
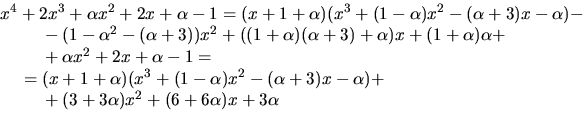
![]()
![]()
![]()
![]()
![]() och
och ![]()