- (a)
- Eftersom polynomet f(x)=x3-3x2+4x-4 är av grad 3
räcker det att undersöka om det har en faktor av grad 1. En
sådan motsvarar ett rationellt nollställe enligt faktorsatsen. De
möjliga rationella nollställena är
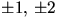 och
och 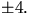 Vi
ser genast att de negativa värdena är uteslutna. Vi har
Vi
ser genast att de negativa värdena är uteslutna. Vi har
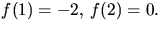 Alltså har f(x) faktorn x-2:
f(x)=(x-2)(x2-x+2). Polynomet är alltså inte irreducibelt.
Alltså har f(x) faktorn x-2:
f(x)=(x-2)(x2-x+2). Polynomet är alltså inte irreducibelt.
- (b)
- Eftersom f(x)=x4+x-3 har grad 4 räcker det
att undersöka om det har faktor av grad 1 eller 2. De möjliga
rationella nollställena är
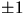 och
och 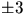 . Vi har
. Vi har 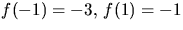 och
och 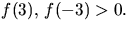 Polynomet saknar alltså faktor av grad
1.
Polynomet saknar alltså faktor av grad
1.
Vi undersäker nu om f(x) har faktor av grad 2 genom att ansätta f(x)=(x2+ax+b)(x2+cx+d), där vi kan förutsätta att
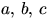 och
och 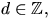 eftersom polynomet är primitivt,
och att
eftersom polynomet är primitivt,
och att 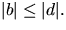 Utveckling ger ekvationssystemet
Utveckling ger ekvationssystemet
Den sista ekvationen ger alternativen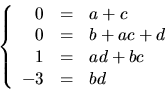
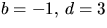 och
och 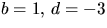 . Första alternativet ger 1=3a-c i tredje ekvationen,
som tillsammans med första ekvationen ger orimlighten a=1/4 (ej
heltal). Andra alternativet ger 1=-3a+c i tredje ekvationen, som
tillsammans med första ekvatioen ger orimlighten a=-1/4. Därmed
är polynomet irreducibelt.
. Första alternativet ger 1=3a-c i tredje ekvationen,
som tillsammans med första ekvationen ger orimlighten a=1/4 (ej
heltal). Andra alternativet ger 1=-3a+c i tredje ekvationen, som
tillsammans med första ekvatioen ger orimlighten a=-1/4. Därmed
är polynomet irreducibelt.
- (c)
- Eftersom primtalet 5 delar samtliga koefficienter utom den
ledande och
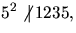 (eftersom
(eftersom 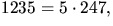 ) är
polynomet irreducibelt enligt Eisensteins kriterium.
) är
polynomet irreducibelt enligt Eisensteins kriterium.
svar: Polynomen i b och c är irreducibla.
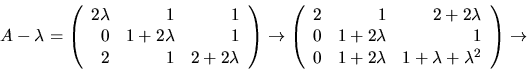
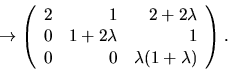
Vi bestämmer egenvektorer hörande till vart och ett av egenvärdena
genom att bestämma en vektor ![]() sådan att
sådan att
![]() Radoperationerna ovan ger
Radoperationerna ovan ger
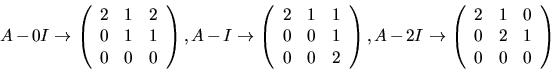
Vi har nu att ![]() där D är
den diagonala matrisen med
där D är
den diagonala matrisen med ![]() och 2 längs
huvuddiagonalen. Sätter vi
och 2 längs
huvuddiagonalen. Sätter vi ![]() har vi att C är inverterbar ty egenvektorerna hör till
olika egenvärden. Vi får AC=CD, dvs A=CDC-1.
har vi att C är inverterbar ty egenvektorerna hör till
olika egenvärden. Vi får AC=CD, dvs A=CDC-1.
svar: A=CDC-1, där
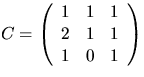 och
och
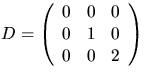 .
.
Eftersom polynomet p(x)=x3+4x+6 är av grad 3 räcker det att
visa att det saknar faktor av grad 1. En sådan motsvarar ett
nollställe i ![]() enligt faktorsatsen. Vi har
enligt faktorsatsen. Vi har
![]()
![]()
Vi bestämmer inversen till ![]() genom att bestämma
en största gemensam delare till p(x) och x2+3x+6 med Euklides
algoritm:
genom att bestämma
en största gemensam delare till p(x) och x2+3x+6 med Euklides
algoritm:
p(x)=(x+4)(x2+3x+6)+3
I![]()
svar: ![]()
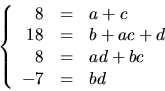
f(x)=(x2+2x-1)(x2+6x+7)
Eftersom faktorerna är irreducibla har vi kroppen
Vi undersöker om x2+6x+7 faktoriserar i K[x] genom att
söka ett nollställe i K. Kvadratkomplettering ger
0=x2+6x+7=(x+3)2-2. Vi sätter ![]()
![]() och ska lösa
och ska lösa ![]() . Detta ger
ekvationssystemet
. Detta ger
ekvationssystemet
![]()
svar: 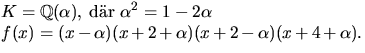
![]()
Vi undersöker om ![]() faktoriserar. Eftersom
faktoriserar. Eftersom ![]() och
p(4)=p(-1)=1 och polynomet är av grad 3 är det irreducibelt
enligt faktorsatsen. Vi har därför att
och
p(4)=p(-1)=1 och polynomet är av grad 3 är det irreducibelt
enligt faktorsatsen. Vi har därför att ![]() om
och endast om xn=1 i
om
och endast om xn=1 i ![]() Vi ska bestämma
ordningen av
Vi ska bestämma
ordningen av ![]() som är en grupp
av ordning
som är en grupp
av ordning ![]() (och 31 är ett
primtal). Enligt Lagranges sats gäller att ordnigen av x delar
(och 31 är ett
primtal). Enligt Lagranges sats gäller att ordnigen av x delar
![]() . Den är alltså
. Den är alltså ![]() eller 124. Den är
uppenbarligen inte 1 eller 2. Vi har
eller 124. Den är
uppenbarligen inte 1 eller 2. Vi har
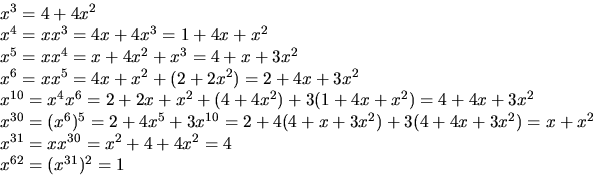
svar: 62.