Därmed är p(x) irreducibelt och ![]() en kropp.
en kropp.
För att bestämma inversen till ![]() använder vi Euklides
algoritm för största gemensamma delaren till polynomen
använder vi Euklides
algoritm för största gemensamma delaren till polynomen
![]() och
och ![]()
![]()
svar: ![]()
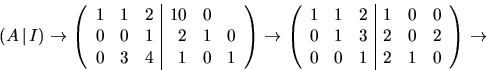
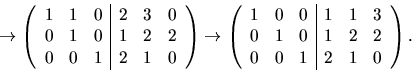

svar:
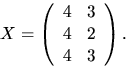
För att lösa ekvationen gör vi först en kvadratkomplettering:
![]() och sätter
och sätter ![]() Vi
ska förstöka bestämma de rationella talen a och b så att
Vi
ska förstöka bestämma de rationella talen a och b så att
![]() Detta ger ekvationssystemet
Detta ger ekvationssystemet
![]()
0=a2+6ab+8b2=(a+3b)2-b2=(a+3b-b)(a+3b+b),
så a=-2b eller -4b. Insättning i den första ekvationen i systemet ger 3b2=3 respektive 15b2=3. Den sista ekvationen saknar rationella lösningar medan den första har lösningarnasvar: ![]()
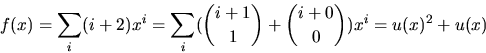
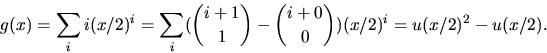
![]()
![]()
Vi har alltså
![]()
svar: ![]()
Uppgiften är att bestämma det minsta värde n, så att
![]() Vi försöker först faktorisera
Vi försöker först faktorisera
![]() Eftersom
Eftersom ![]() saknar p(x) irreducibla faktorer av grad 1 och 3. Vi ansätter
p(x)=(x2+ax+b)(x2+cx+d) och får ekvationssystemet:
saknar p(x) irreducibla faktorer av grad 1 och 3. Vi ansätter
p(x)=(x2+ax+b)(x2+cx+d) och får ekvationssystemet:
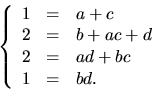
Detta ger att ![]() om och endast om
om och endast om
![]() ty p(x) har inte 1+2x som faktor.
Vi ska bestämma det minsta n så att
ty p(x) har inte 1+2x som faktor.
Vi ska bestämma det minsta n så att
![]() dvs
dvs ![]() Vi ska alltså bestämma ordningen av
Vi ska alltså bestämma ordningen av ![]() Gruppen
Gruppen ![]() består av
alla polynom av grad
består av
alla polynom av grad ![]() som är relativt prima med p(x), dvs
som inte delas av x2+2x+2. Det finns 34 polynom av grad
som är relativt prima med p(x), dvs
som inte delas av x2+2x+2. Det finns 34 polynom av grad
![]() i
i ![]() De som inte är relativt prima med
x2+2x+2 är ett förstagradspolynom gånger det. Det finns 32
sådana. Gruppen består av 34-32=72 element. Enligt Lagranges
sats delar ordingen av x talet
De som inte är relativt prima med
x2+2x+2 är ett förstagradspolynom gånger det. Det finns 32
sådana. Gruppen består av 34-32=72 element. Enligt Lagranges
sats delar ordingen av x talet ![]() Den är alltså
Den är alltså
![]() eller 72. Eftersom
p inte kan dela 1-xn om
eller 72. Eftersom
p inte kan dela 1-xn om ![]() kan de första alternativen
uteslutas.
kan de första alternativen
uteslutas.
Vi räknar modulo p(x) och har
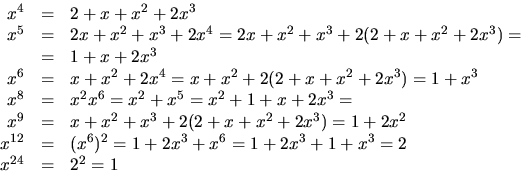
svar: 24.