![]()
svar: ![]() och
och ![]()
Radoperationer ger:
![]()
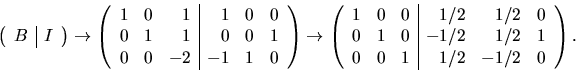
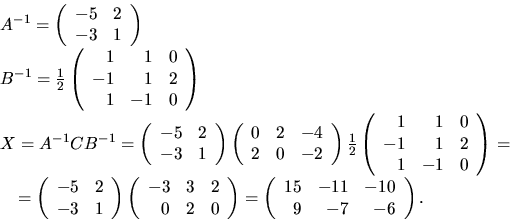
svar: 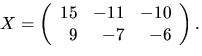
Vi skriver om f med hjälp av u och utnyttjar att
![]()
![]()
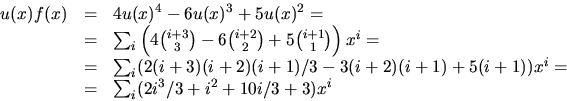
svar: Summan är (2n3+3n2+10n+9)/3.
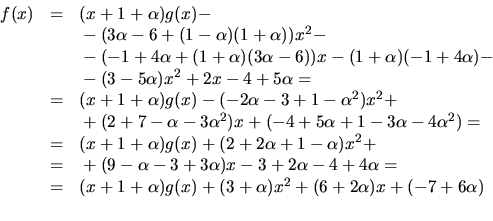
![]()
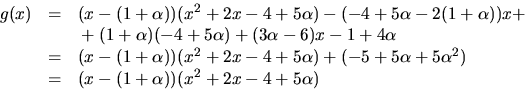
Kvadratkomplettering ger
![]()
![]()
svar: ![]() och
och ![]()
![]()
![]()
Vi bestämmer en största gemensam delare till p(x) och 4+x med Euklides algoritm:
![]()
Vi faktoriserar först q(x). Vi ser att x=2 är ett nollställe. Faktorisering enligt Faktorsatsen ger
q(x)=(x-2)(x2+3x+4)=(x+3)(x2+3x+4)
Polynomet x2+3x+4 saknar nollställe och är därför irreducibelt eftersom det är av grad 2.
Ringen ![]() består av alla poynom av grad
består av alla poynom av grad ![]() samt 0. Den innehåller alltså 53=125 element. Gruppen
samt 0. Den innehåller alltså 53=125 element. Gruppen ![]() består av alla polynom av grad
består av alla polynom av grad ![]() som är
relativt prima med q(x). De som inte är relativt prima med q(x)
delas av x+3 eller x2+3x+4. Det finns 52 polynom
(av grad
som är
relativt prima med q(x). De som inte är relativt prima med q(x)
delas av x+3 eller x2+3x+4. Det finns 52 polynom
(av grad ![]() eller =0) som delas av x+3. Det
finns 5 som delas av x2+3x+4. Bara 0 delas av båda. Detta ger
att gruppen innehåller
eller =0) som delas av x+3. Det
finns 5 som delas av x2+3x+4. Bara 0 delas av båda. Detta ger
att gruppen innehåller ![]()
Enligt Lagranges sats
delar ordingen av x talet 96, dvs den är ![]()
![]() eller 96.
Den är inte 1 eller 2, ty
eller 96.
Den är inte 1 eller 2, ty ![]() I ringen gäller att
0=x3+x2+3x+2. Detta ger
I ringen gäller att
0=x3+x2+3x+2. Detta ger
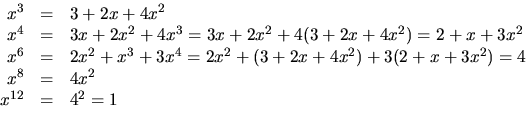
svar: 12.