Lösningar till tentamen i Aritmetik och algebra, del
2, 98 xx 04.
- 4.
- Det gäller att visa att
![$p(x)=x^{4}-3x+4\in \mathbb Q[x]$](img1.gif) är
irreducibelt. Eftersom polynomet är primitivt och av grad 4 räcker
det att visa att det saknar faktorer av grad 1 och 2 i
är
irreducibelt. Eftersom polynomet är primitivt och av grad 4 räcker
det att visa att det saknar faktorer av grad 1 och 2 i ![$\mathbb
Z[x]$](img2.gif) .
En faktor av grad 1 motsvarar ett nollställe enligt faktorsatsen. De
möjliga rationella nollställena är
.
En faktor av grad 1 motsvarar ett nollställe enligt faktorsatsen. De
möjliga rationella nollställena är 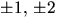 och
och 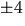 . Vi
ser genast att de negativa värdena är uteslutna. Vi har p(1)=2,
p(2)=14 och p(4)>0. Inget duger så polynomet saknar faktor av grad
1.
. Vi
ser genast att de negativa värdena är uteslutna. Vi har p(1)=2,
p(2)=14 och p(4)>0. Inget duger så polynomet saknar faktor av grad
1.
Vi undersöker faktorer av grad 2 genom att ansätta
p(x)=
(x2+ac+b)(x2+cx+d), där 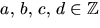 .
Vi kan också förutsätta att
.
Vi kan också förutsätta att 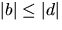 .Utveckling ger ekvationssystemet
.Utveckling ger ekvationssystemet
![\begin{displaymath}
\left\{
\begin{array}[c]
{rcl}
0&=&a+c\\ 0&=&b+ac+d\\ -3&=&ad+bc\\ 4&=&bd\end{array}\right.\end{displaymath}](img7.gif)
Den sista ekvationen ger alternativen 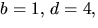
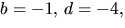 b=2=d=2 och b=d=-2. Det första alternativet ger -3=4a+c i den
tredje ekvationen. Tillsammans med den första ger detta
b=2=d=2 och b=d=-2. Det första alternativet ger -3=4a+c i den
tredje ekvationen. Tillsammans med den första ger detta 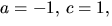 vilket strider mot den andra ekvationen. Alternativet
vilket strider mot den andra ekvationen. Alternativet 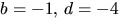 ger 3=4a+c i tredje ekvationen. Med den första ger detta
ger 3=4a+c i tredje ekvationen. Med den första ger detta
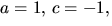 vilket strider mot den andra ekvationen. Alternativen
vilket strider mot den andra ekvationen. Alternativen
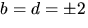 ger
ger 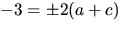 i tredje ekvationen, vilket strider
mot den första. Ekvationssystemet saknar alltså lösning och därför
saknar p(x) också faktor av grad 2. Alttså är p(x) irreducibelt
och
i tredje ekvationen, vilket strider
mot den första. Ekvationssystemet saknar alltså lösning och därför
saknar p(x) också faktor av grad 2. Alttså är p(x) irreducibelt
och 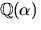 en kropp.
en kropp.
För att invertera 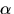 använder vi Euklides algoritm:
använder vi Euklides algoritm:
![\begin{displaymath}
\begin{array}[c]
{rcl}
0=\alpha^{4}-3\alpha+4&=&(\alpha^{3}-3)\alpha+4\\ \end{array}\end{displaymath}](img17.gif)
Detta ger 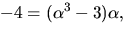 dvs
dvs 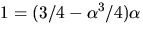 .
.svar: 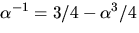
- 5.
- Vektorerna
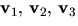 och
och
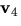 är linjärt oberoende om matrisen
är linjärt oberoende om matrisen 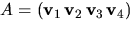 har rang 4.
Rad- och kolonnoperatioer (markerade med r resp k) ger
har rang 4.
Rad- och kolonnoperatioer (markerade med r resp k) ger
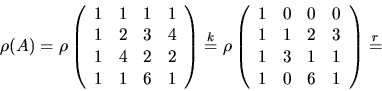
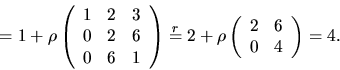
Därmed är vektorerna linjärt oberoende.
- 6.
- Vi skriver om f(x) med hjälp av
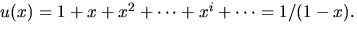 Vi har f(x)=1+x+u(x).
Vi får
Vi har f(x)=1+x+u(x).
Vi får
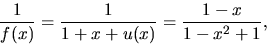
där den sista likheten får genom förlängning med 1-x.
Partialbråksuppdelning ger
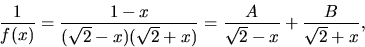
där A och B bestäms med handpåläggning till 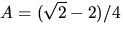 respektive
respektive 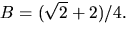 Vi får
Vi får
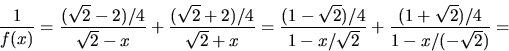
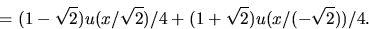
dvs
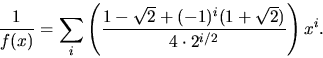
svar: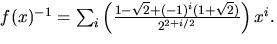
- 7.
- Vi undersöker först om f(x)=x3+2x+4 kan faktoriseras med
koefficienter i
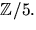 Eftersom polynomet är av grad 3
räcker det enligt faktorsatsen att undersöka eventuella nollställen i
Eftersom polynomet är av grad 3
räcker det enligt faktorsatsen att undersöka eventuella nollställen i
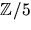 . Insättning av
. Insättning av 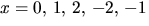 ger i tur och
ordning
ger i tur och
ordning 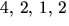 och 1. Därmed är f(x) irreducibelt i
och 1. Därmed är f(x) irreducibelt i
![$\mathbb Z/5[x].$](img39.gif)
Vi får därför kroppen ![$K=\mathbb Z/5[x]/f(x)=\mathbb Z/5(\alpha),$](img40.gif) där
där 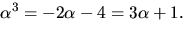 f(x) har nollstället
f(x) har nollstället
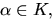 men eftersom
men eftersom 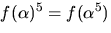 även
nollstället
även
nollstället 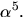 Vi beräknar
Vi beräknar 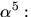
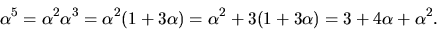
Enligt faktorsatsen delas f(x) av
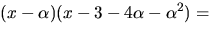
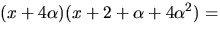
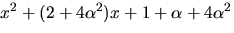 Divisonen ger
Divisonen ger
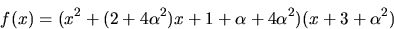
svar: 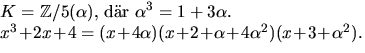
- 8.
- Sätt
 Om f(x) multipliceras med
u(x)=1/(1-x) fås en potensserie vars koefficient framför xn
är den sökta summan. Vi skriver om f(x) med hjälp av u(x) och
utnyttjar att
Om f(x) multipliceras med
u(x)=1/(1-x) fås en potensserie vars koefficient framför xn
är den sökta summan. Vi skriver om f(x) med hjälp av u(x) och
utnyttjar att 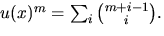 Vi har
Vi har
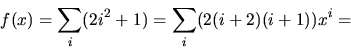
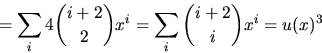
Koefficienten framför xn i f(x)u(x)=u(x)4 är alltså
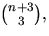 dvs
dvs
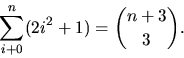
svar: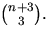
![]() .
Vi kan också förutsätta att
.
Vi kan också förutsätta att ![]() .Utveckling ger ekvationssystemet
.Utveckling ger ekvationssystemet
![\begin{displaymath}
\left\{
\begin{array}[c]
{rcl}
0&=&a+c\\ 0&=&b+ac+d\\ -3&=&ad+bc\\ 4&=&bd\end{array}\right.\end{displaymath}](img7.gif)
![]() använder vi Euklides algoritm:
använder vi Euklides algoritm:
![]()
![]()
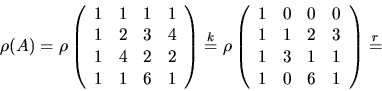
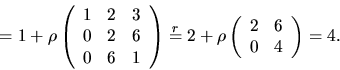
![]()
![]()
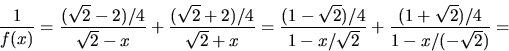
![]()
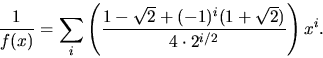
![]()
![]() där
där ![]() f(x) har nollstället
f(x) har nollstället
![]() men eftersom
men eftersom ![]() även
nollstället
även
nollstället ![]() Vi beräknar
Vi beräknar ![]()
![]()
![]()
![]()
![]() Divisonen ger
Divisonen ger
![]()
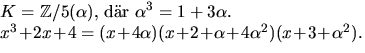
![]()
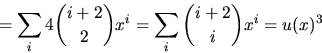
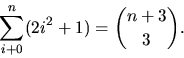
![]()