Lösningar till tentamen i Aritmetik och algebra, del
2, 98 xx 05.
- 4.
- Det gäller att visa att
![$p(x)=x^{3}-2x-5=x^{3}+5x+2\in \mathbb Z/7[x]$](img1.gif) är
irreducibelt. Eftersom polynomet har grad 3 räcker det att visa att
det saknar nollställe i
är
irreducibelt. Eftersom polynomet har grad 3 räcker det att visa att
det saknar nollställe i 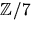 enligt Faktorsatsen. Vi har
enligt Faktorsatsen. Vi har
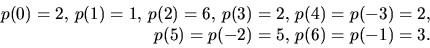
Därmed är p(x) irreuducibelt och 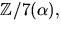 där
där
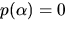 en kropp.
För att bestämma inversen till
en kropp.
För att bestämma inversen till 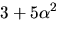 använder vi Euklides
alogritm för en största gemensam delare till polynomen
använder vi Euklides
alogritm för en största gemensam delare till polynomen 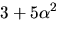 och
och 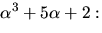
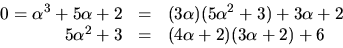
Baklänges ger detta
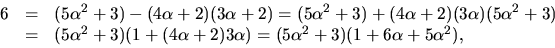
så 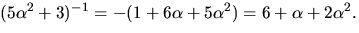 svar:
svar: 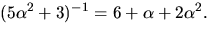
- 5.
- Det gäller att visa att
![$p(x)=x^{3}-x-1\in \mathbb Q[x]$](img12.gif) är
irreducibelt. Eftersom polynomet är av grad 3 räcker det att visa
att det saknar rationellt nollställe, enligt Faktorsatsen. De möjliga
rationella nollställena är
är
irreducibelt. Eftersom polynomet är av grad 3 räcker det att visa
att det saknar rationellt nollställe, enligt Faktorsatsen. De möjliga
rationella nollställena är 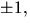 men inget duger. Därmed är p(x)
irreducibelt och
men inget duger. Därmed är p(x)
irreducibelt och 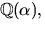 där
där 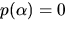 en kropp.
en kropp.
Vi vet att 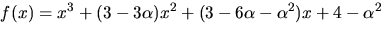 har nollställena
har nollställena 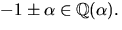 Enligt
faktorsatsen delas f(x) av
Enligt
faktorsatsen delas f(x) av
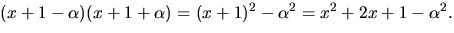 Vi bestämmer kvoten genom division:
Vi bestämmer kvoten genom division:
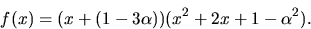
Det återstående nollstället är alltså 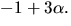
svar: 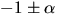 och
och 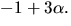
- 6.
- Vi försöker diagonalisera A och söker därför egenvärden, dvs värden
på
 så att rangen av
så att rangen av 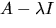 är
är 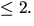 Vi gör
radoperationer:
Vi gör
radoperationer:
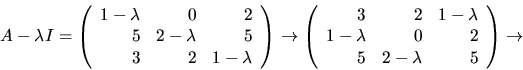
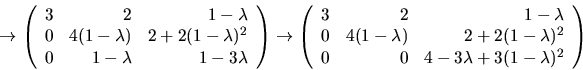
Vi ser att rangen är 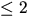 om
om 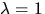 eller om
eller om
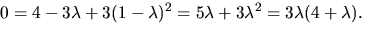 Egenvärdena är alltså
Egenvärdena är alltså 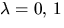 och 3.
och 3.
Vi bestämmer en egenvektor hörande till vart och ett av dessa
egenvärden (genom att anväda räkningarna ovan):
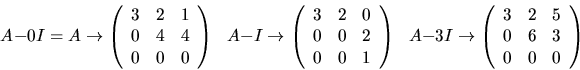
Vi har (t.ex.) egenvektorerna 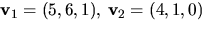 och
och 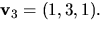 Vi har alltså att
Vi har alltså att
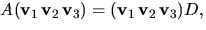 eller AC=CD, där
eller AC=CD, där
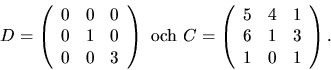
Eftersom kolonnerna i C hör till olika egenvärden är de linjärt
oberoende och C har därför rang 3 och är därmed inverterbar. Vi
har A=CDC-1 och An=CDnC-1. Eftersom
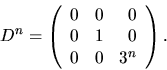
återstår det att bestämma C-1 innan vi kan bestämma An.
Vi gör radoperationer på 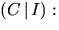
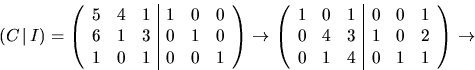
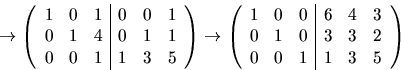
Detta ger att C-1 är den högra halvan av matrisen.
Vi har nu
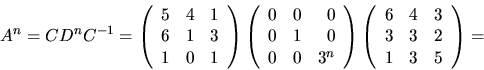
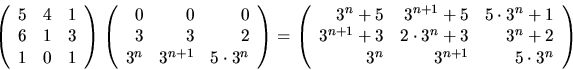
svar: Se ovan.
- 7.
- Rekursionsekvationens karaktäristiska polynom är
q(x)=x3-x2+x-1=(x-1)(x2+1)=(x-1)(x-i)(x+i), med nollställena
1 och
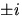 av multiplicitet 1.
Den allmänna lösningen till rekursionsekvationen
av multiplicitet 1.
Den allmänna lösningen till rekursionsekvationen
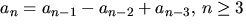 ges därför av
ges därför av
an=A1n+Bin+C(-i)n,
där 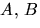 och C ska bestämmas så att
och C ska bestämmas så att 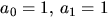 och
a2=2. Detta ger ekvationssystemet
och
a2=2. Detta ger ekvationssystemet
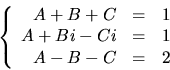
med lösning  och C=(-1-i)/4.
och C=(-1-i)/4.
svar: an=(6+(-1+i)in-(1+i)(-i)n)/4.
- 8.
- Vi skriver om f och g med hjälp av
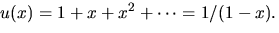 Vi har
Vi har
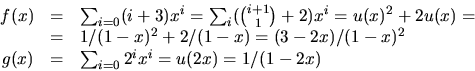
och får:
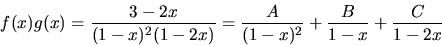
där A och C bestäms med handpålggning till 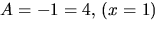 och
och
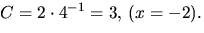 Sätter vi x=0 får vi 3=A+B+C=2+B, så
B=1. Detta ger
Sätter vi x=0 får vi 3=A+B+C=2+B, så
B=1. Detta ger
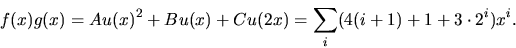
svar: 
![]()
![]()
![]()
![]() har nollställena
har nollställena ![]() Enligt
faktorsatsen delas f(x) av
Enligt
faktorsatsen delas f(x) av
![]() Vi bestämmer kvoten genom division:
Vi bestämmer kvoten genom division:
![]()
![]() och
och ![]()
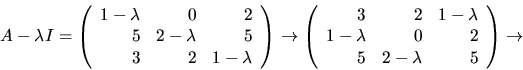
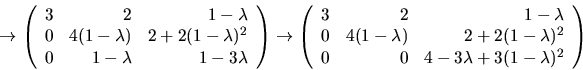
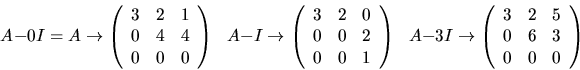
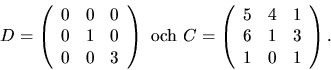
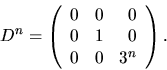
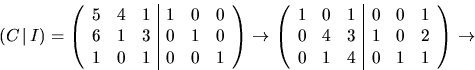
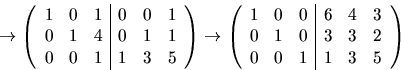
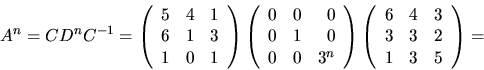
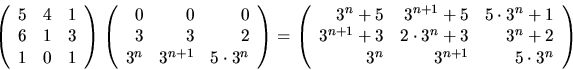
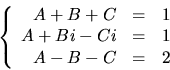
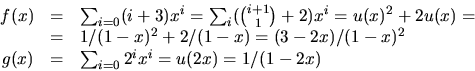
![]()
![]()
![]()