- 4.
- Vi försöker faktorisera nämnaren g(x)=x4+2x3+5x2+6x+6. De möjliga
rationella nollställena är
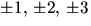 och
och 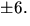 De
positiva talen är uteslutna. Vi har
De
positiva talen är uteslutna. Vi har 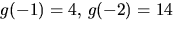 och
och
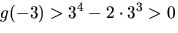 samt
samt 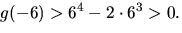 Rationellt nollställe saknas. Vi försöker faktorisera som produkt av
två rationella polynom av grad 2. Ansätt
g(x)=(x2+ax+b)(x2+cx+d), där
Rationellt nollställe saknas. Vi försöker faktorisera som produkt av
två rationella polynom av grad 2. Ansätt
g(x)=(x2+ax+b)(x2+cx+d), där 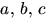 och
och 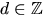 (polynometär primitivt). Vi får ekvationssystemet
(polynometär primitivt). Vi får ekvationssystemet
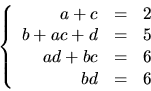
Sista ekvationen ger att b och d delar 6. En genomgång av
möjligheterna ger att 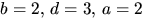 och c=0 löser
ekvationssystemet. Vi har alltså g(x)=(x2+2x+2)(x2+3).
Partialbråk med rationella koefficienter ger ansatsen
och c=0 löser
ekvationssystemet. Vi har alltså g(x)=(x2+2x+2)(x2+3).
Partialbråk med rationella koefficienter ger ansatsen
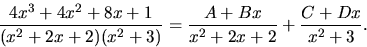
Hopmultiplicering av ansatsen och jämförelse av koefficienter ger
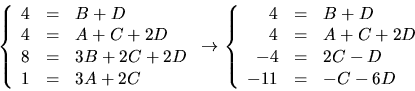
med lösning 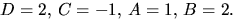
svar: (1+2x)/(x2+2x+2)+(2x-1)/(x2+3).
- 5.
- Vi söker egenvärden till A genom att bestämma värden på
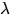 så
att rangen av
så
att rangen av 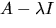 är
är 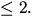 Radoperationer ger
Radoperationer ger
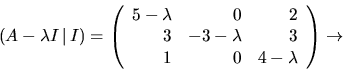
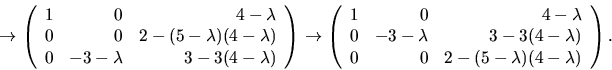
Vi ser att rangen är 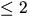 om
om 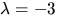 och
och
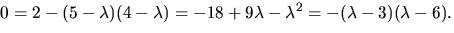 Egenvärdena är alltså
Egenvärdena är alltså 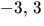 och 6.
och 6.
Vi söker egenvektorer hörande till vart och ett av dessa egenvärden
och utnyttjar räkningen ovan:
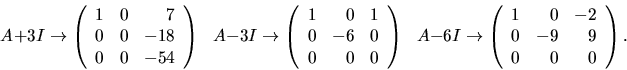
Vi får (t.ex.) egenvektorerna 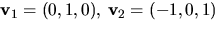 respektive
respektive 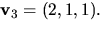
Sätter vi 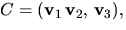 så är
C inverterbar ty vektorerna är linjärt oberoende eftersom de hör
till olika egenvärden. Sätter vi
så är
C inverterbar ty vektorerna är linjärt oberoende eftersom de hör
till olika egenvärden. Sätter vi
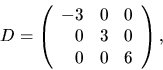
så har vi A=CDC-1.
svar: Se ovan.
- 6.
- Sätter vi p(x)=1-4x-2x2=1+x+3x2 har vi att
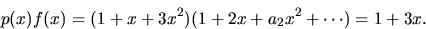
Detta ger f(x)=(1+3x)/p(x) och därmed 1/f(x)=p(x)/(1+3x).
Division ger 3x2+x+1=x(3x+1)+1. Vi får
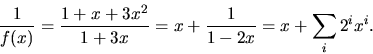
svar: 
- 7.
- Koefficienten framför xn i
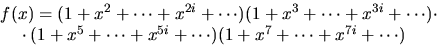
är antalet sätt att skriva n som en summa av talen 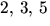 och
7. Potensserien f(x) är alltså problemets genererande funktion.
och
7. Potensserien f(x) är alltså problemets genererande funktion.
Om vi sätter p(x)=(1-x2)(1-x3)(1-x5)(1-x7) gäller att
f(x)=1/p(x), dvs p(x)f(x)=1. Utveckling av p(x) ger
p(x)=(1-x2-x3+x5)(1-x5-x7+x12)=1-x2-x3+x8+
x9-x14-x15+x17
Koefficienterna an i f(x) uppfyller därför sambandet
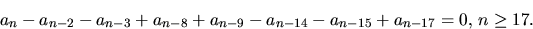
Svar: 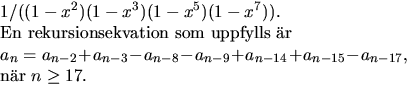
- 8.
- För att visa att ringen är en kropp ska vi visa att
![$p(x)=x^{2}-x-3\in
\mathbb Q[x]$](img34.gif) är irreducibelt. Eftersom polynomet är av grad 2 är
detta samma sak som att visa att det saknar rationellt nollställe
enligt Faktorsatsen. De möjliga rationella nollställena är
är irreducibelt. Eftersom polynomet är av grad 2 är
detta samma sak som att visa att det saknar rationellt nollställe
enligt Faktorsatsen. De möjliga rationella nollställena är 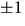 och
och
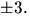 Vi har
Vi har 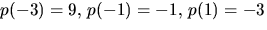 och p(3)=3. Inget av
de möjliga rationella nollställena duger. Därmed är p(x)
irreducibelt och
och p(3)=3. Inget av
de möjliga rationella nollställena duger. Därmed är p(x)
irreducibelt och 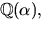 där
där 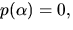 är en kropp.
är en kropp.
Vi löser ekvationen genom att först göra en kvadratkomplettering:
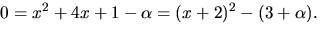 Om vi sätter
Om vi sätter
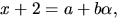 där
där 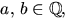 ska vi alltså lösa
ekvationen
ska vi alltså lösa
ekvationen 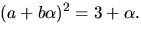 Utveckling av vänstra ledet ger
ekvationssystemet
Utveckling av vänstra ledet ger
ekvationssystemet
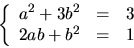
Multiplikation av den nedre ekvationen med -3 och addtion av
resultatet till den övre ger 0=a2-6ab=a(a-6b), så a=0 eller
a=6b. Det sista alternativet ger 13b2=1, som saknar rationell
lösning. Det första alternativet ger 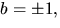 som duger. Vi får
alltså
som duger. Vi får
alltså 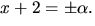
Svar: 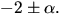
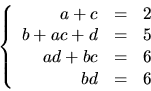
![]()
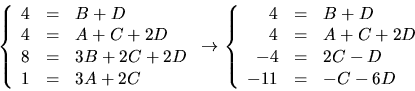
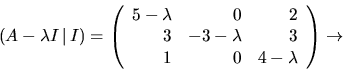
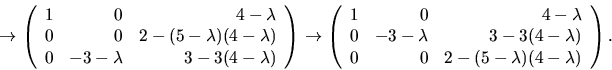
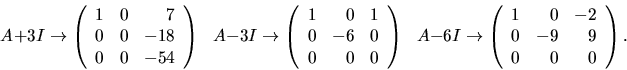
![]() så är
C inverterbar ty vektorerna är linjärt oberoende eftersom de hör
till olika egenvärden. Sätter vi
så är
C inverterbar ty vektorerna är linjärt oberoende eftersom de hör
till olika egenvärden. Sätter vi
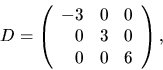
![]()
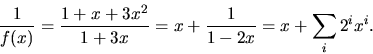
![]()
![]()
![]()
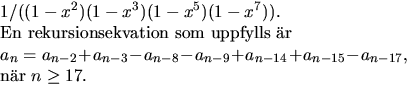
![]() Om vi sätter
Om vi sätter
![]() där
där ![]() ska vi alltså lösa
ekvationen
ska vi alltså lösa
ekvationen ![]() Utveckling av vänstra ledet ger
ekvationssystemet
Utveckling av vänstra ledet ger
ekvationssystemet
![]()
![]()