- 1.
- Vi undersöker först för vilka värden på u som
f(x)=x4+3x3+ux2-1 har en faktor av grad 1 i
![$\mathbb Q[x]$](img2.gif) . Enligt
faktorsatsen motsvaras en sådan av ett rationellt nollställe. Eftersom
f(x) har heltalskoefficienter är de möjliga rationella
nollställena a/b där
. Enligt
faktorsatsen motsvaras en sådan av ett rationellt nollställe. Eftersom
f(x) har heltalskoefficienter är de möjliga rationella
nollställena a/b där 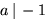 och
och 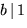 . Detta ger
. Detta ger 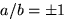 . Vi har
. Vi har
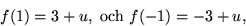
så f(x) har en faktor av grad 1 när 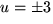 . För dessa värden
har vi
. För dessa värden
har vi
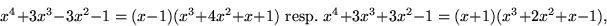
där de två polynomen av grad 3 är irreducibla. De saknar nämligen rationella
nollställen (de möjliga är 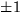 ) och därmed faktor av såväl grad
1 som 2.
Vi undersöker för vilka värden på u som f(x) har en faktor av grad
2. Vi ansätter
) och därmed faktor av såväl grad
1 som 2.
Vi undersöker för vilka värden på u som f(x) har en faktor av grad
2. Vi ansätter
f(x)=(x2+ax+b)(x2+cx+d)
där vi kan förutsätta att 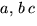 och d är heltal eftersom
f(x) är primitivt och att
och d är heltal eftersom
f(x) är primitivt och att 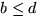 . Identifiering av koefficienter ger att vi ska
undersöka för vilka värden på u som ekvationssystemet
. Identifiering av koefficienter ger att vi ska
undersöka för vilka värden på u som ekvationssystemet
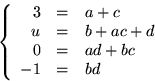
har lösning.Den nedersta ekvationen ger b=-1 och d=1 (vi använder
att 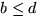 ). Detta ger ekvationssystemet
). Detta ger ekvationssystemet
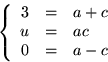
Summan av den första och sista ekvationen ger 3=2a som är olösbar
med 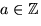 . Polynomet f(x) saknar alltså faktor av grad
2 för varje värde på heltalet u.
. Polynomet f(x) saknar alltså faktor av grad
2 för varje värde på heltalet u.
Svar: Polynomet är irreducibelt om 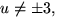 medan
x4+3x3-3x2-1=(x-1)(x3+4x2+x+1) och
x4+3x3+3x2-1=(x+1)(x3+2x2+x-1).
medan
x4+3x3-3x2-1=(x-1)(x3+4x2+x+1) och
x4+3x3+3x2-1=(x+1)(x3+2x2+x-1).
- 2.
- Vi faktoriserar först nämnaren, som har heltalskoefficienter och därför
de möjliga rationella nollställena a/b där
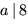 och
och 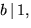 så
så  och
och  . Prövning ger att 2
duger. Faktorsatsen ger
. Prövning ger att 2
duger. Faktorsatsen ger
x4+2x3-18x2+16x+8=(x-2)(x3+4x2-10x-4)=(x-2)2(x2+6x+2)
där polynomet x2+6x+2 är irreducibelt (t.ex. enligt Eisensteins
kriterium med p=2). Enligt satserna om partialbråksuppdelning finns
rationella tal 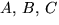 och D så att
och D så att
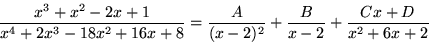
Handpåläggning ger
A=9/18=1/2
Insättning av 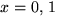 respektive -1 ger ekvationssystemet
respektive -1 ger ekvationssystemet
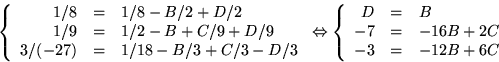
De två nedersta ekvationerna ger B=C=1/2.
Svar: (1/2)(1/(x-2)2+1/(x-2)+(x+1)/(x2+6x+2)).
- 3.
- Vi har att
![$g(x)\in \mathbb Q[x]/(x^{3}-4x-3)$](img24.gif) är inverterbart om och
endast om
är inverterbart om och
endast om  där f(x)=x3-4x-3.
där f(x)=x3-4x-3.
- (a)
- Eftersom g(x)=x+1 är irreducibelt är
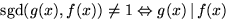 . Enligt
faktorsatsen är detta ekvivialent med att f(-1)=0. Vi har
f(-1)=0, så x+1 är inte inverterbart.
. Enligt
faktorsatsen är detta ekvivialent med att f(-1)=0. Vi har
f(-1)=0, så x+1 är inte inverterbart.
- (b)
- Eftersom f(1)=-6 är g(x)=x-1 inverterbart (se a)). Vi bestämmer
en invers med hjälp av Euklides algoritm:
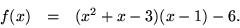
I ![$\mathbb Q[x]/(x^{3}-4x-3)$](img28.gif) ger detta
ger detta
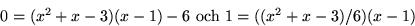
så inversen till x-1 är (x2+x-3)/6.
- (c)
- Vi bestämmer
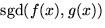 där g(x)=x2-x med Euklides
algoritm:
där g(x)=x2-x med Euklides
algoritm:
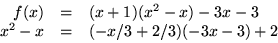
I ![$\mathbb Q[x]/(x^{3}-4x-3)$](img28.gif) ger detta
ger detta
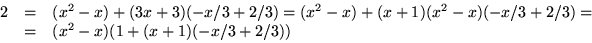
Detta ger 1=(x2-x)(-x2/6+x/6+5/6) så inversen till x2-x
är (-x2+x+5)/6.
Svar: x+1 är inte inverterbar, x-1 är inverterbar med invers
(x2+x-3)/6 och x2-x är inverterbar med invers (-x2+x+5)/6.
- 4.
- Kvadratkomplettering ger att vi ska lösa
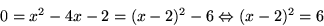
Elementen i  är av formen
är av formen 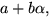 där
där
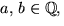 eftersom vi räknar modulo andragradspolynomet
eftersom vi räknar modulo andragradspolynomet
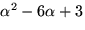 . Vi sätter
. Vi sätter
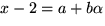 och ska lösa
och ska lösa 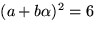 . Utveckling och
utnyttjande av
. Utveckling och
utnyttjande av 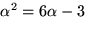 ger
ger
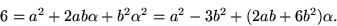
Detta ger ekvationssystemet
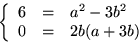
Den nedersta ekvationen ger b=0 eller a=-3b. Det första
alternativet ger 6=a2 i första ekvationen. Denna saknar rationell
lösning. Det andra alternativet ger 6=6b2 som har lösningarna
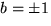 . Vi får alltså
. Vi får alltså  och
och
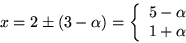
Svar: 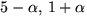 .
.
![]()
![]()
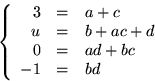
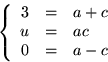
![]() medan
x4+3x3-3x2-1=(x-1)(x3+4x2+x+1) och
x4+3x3+3x2-1=(x+1)(x3+2x2+x-1).
medan
x4+3x3-3x2-1=(x-1)(x3+4x2+x+1) och
x4+3x3+3x2-1=(x+1)(x3+2x2+x-1).
![]()
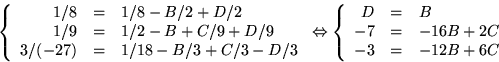
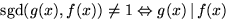 . Enligt
faktorsatsen är detta ekvivialent med att f(-1)=0. Vi har
f(-1)=0, så x+1 är inte inverterbart.
. Enligt
faktorsatsen är detta ekvivialent med att f(-1)=0. Vi har
f(-1)=0, så x+1 är inte inverterbart.
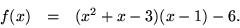
![$\mathbb Q[x]/(x^{3}-4x-3)$](img28.gif) ger detta
ger detta
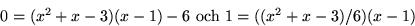
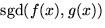 där g(x)=x2-x med Euklides
algoritm:
där g(x)=x2-x med Euklides
algoritm:
![$\mathbb Q[x]/(x^{3}-4x-3)$](img28.gif) ger detta
ger detta
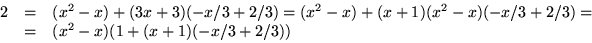
![]()
![]()
![]()
![]()
![]() .
.