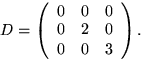För att undersöka om f(x) har en faktor av grad 2 ansätter vi
f(x)=(x2+ax+b)(x2+cx+d), där vi kan förutsätta att ![]() och att
och att ![]() och d är heltal, eftersom f(x) är primitivt.
Identifiering av koefficienter ger ekvationssystemet
och d är heltal, eftersom f(x) är primitivt.
Identifiering av koefficienter ger ekvationssystemet
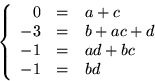
Därmed är f(x) irreducibelt i ![]() och
och ![]() där
där ![]() en kropp.
en kropp.
För att invertera ![]() använder vi Euklides algoritm:
använder vi Euklides algoritm:
![]()
![]()
- (a)
- Vi undersöker först om f(x)=x4-3x3+3x+1 faktoriserar i
![$\mathbb Q[x]$](img9.gif) . Eftersom det har grad 4 räcker det att undersöka
om det har faktorer av grad 1 eller 2.
. Eftersom det har grad 4 räcker det att undersöka
om det har faktorer av grad 1 eller 2.
En faktor av grad 1 motsvarar ett rationellt nollställe. De möjliga rationella nollställena till f(x) är
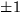 . Inget duger.
. Inget duger.
För att undersöka om f(x) har en faktor av grad 2 ansätter vi f(x)=(x2+ax+b)(x2+cx+d), där vi kan förutsätta att
 och att
och att 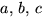 och d är heltal, eftersom f(x) är
primitivt. Identifiering av koefficienter ger ekvationssystemet
och d är heltal, eftersom f(x) är
primitivt. Identifiering av koefficienter ger ekvationssystemet
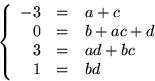
Den nedersta ekvationen ger b=d=1 eller b=d=-1. Det första alternativet ger 3=a+c i tredje ekvationen, vilket strider mot den första. Det andra alternativet ger 2=ac i andra ekvationen, d.v.s
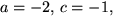
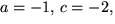
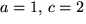 eller
eller  . Kontroll
visar att
. Kontroll
visar att 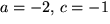 duger. Vi har alltså
duger. Vi har alltså
f(x)=(x2-2x-1)(x2-x-1)
där faktorerna är irreducibla eftersom f(x) saknar faktor av grad 1.Vi har därför kroppen
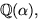 där
där
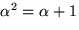 . I
. I ![$\mathbb Q(\alpha)[x]$](img23.gif) gäller att
gäller att
Vi undersöker om x2-2x-1 har något nollställe i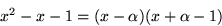
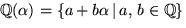 :
:
0=x2-2x-1=(x-1)2-2.
Sätt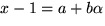 och ekvationen blir
och ekvationen blir
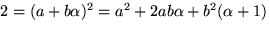 . Detta ger
ekvationssystemet
. Detta ger
ekvationssystemet
Den nedersta ekvationen ger b=0 eller b=-2a. Det första alternativet ger i första ekvationen 2=a2 medan det andra ger 2=5a2. Båda saknar rationella lösningar.
Polynomet x2-2x-1 saknar alltså nollställe i
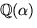 och är
därför irreducibelt i
och är
därför irreducibelt i ![$\mathbb Q(\alpha)[x]$](img23.gif) enligt Faktorsatsen.
enligt Faktorsatsen.
Vi har därför kroppen
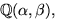 där
där
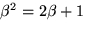 och
och 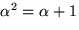 .Vi har
.Vi har
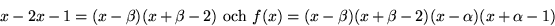
- (b)
- Vi undersöker om f(x)=x3+2x+1 faktoriserar i
![$\mathbb
Z/3[x]$](img33.gif) . Eftersom f(x) har grad 3 räcker det att undersöka om
det har faktorer av grad 1.
. Eftersom f(x) har grad 3 räcker det att undersöka om
det har faktorer av grad 1.
En faktor av grad 1 motsvarar ett nollställe i
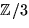 . Men
. Men
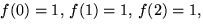 så nollställe saknas.
så nollställe saknas.
Därmed är
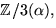 där
där 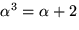 en kropp
i vilken f(x) har nollstället
en kropp
i vilken f(x) har nollstället  . Eftersom
f(x)3=f(x3) är även
. Eftersom
f(x)3=f(x3) är även 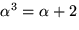 och
och 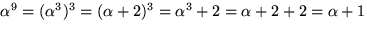 nollställen till f(x). Faktorsatsen ger att
nollställen till f(x). Faktorsatsen ger att
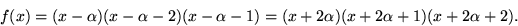
Svar: a) ![]() där
där ![]() och
och ![]() och
och
![]() b)
b)
![]() där
där ![]() och
och ![]() .
.
Vi beräknar A-1 genom att göra radoperationer på (A|I) till (I|I'). Då är I'=A-1.
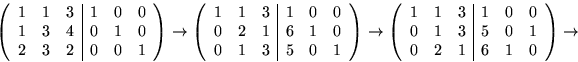

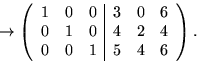
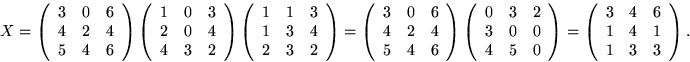
Svar: 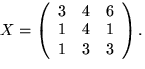
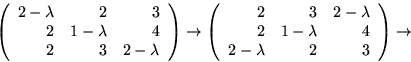
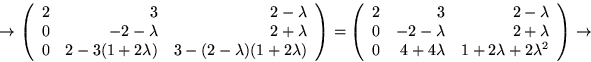
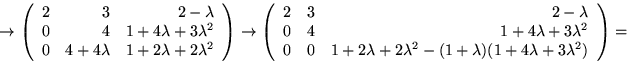

Vi ser att
![]()
Egenvärdena till A är alltså ![]() och 3.
och 3.
Vi bestämmer en egenvektor hörande till
![]() och
och ![]() genom att bestämma
genom att bestämma
![]() så att
så att ![]() . Radoperationerna ovan ger:
. Radoperationerna ovan ger:
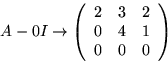
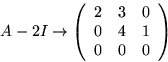
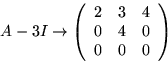
Vi har alltså
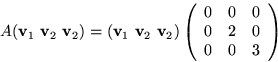
Matrisen ![]() är
inverterbar eftersom vektorerna hör till olika egenvärden.
är
inverterbar eftersom vektorerna hör till olika egenvärden.
Vi har alltså att
A=CDC-1
Svar: 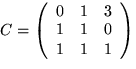 och
och