


Next: About this document ...
Tentamen i MAN011 Aritmetik och algebra, del 2, 98 04 04.
- 1.
- Formulera och bevisa faktorsatsen för polynom i K[x], där K är en kropp.
- 2.
- (a)
- Låt K vara en kropp.
Vad menas med att vektorerna
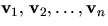 i Km är linjärt oberoende?
i Km är linjärt oberoende?
- (b)
- Låt A vara en
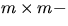 matris med element i kroppen K.
Visa att om
matris med element i kroppen K.
Visa att om 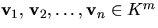 är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
- 3.
- Formulera och bevisa Eisensteins kriterium.
- 4.
- Matrisen X med element i
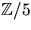 har egenskapen att AX=B, där
har egenskapen att AX=B, där
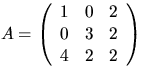 och
och
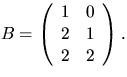
Bestäm X.
- 5.
- Visa att
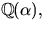 där
där 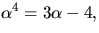 är en kropp
och invertera elementet
är en kropp
och invertera elementet 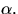
- 6.
- Bestäm en så liten kropp K som möjligt, som innehåller
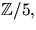 så att
så att ![$x^4+3x^2+3\in
\mathbb Z/5[x]$](img11.gif) faktoriserar som en produkt av polynom av grad 1 i
K[x]. Ange faktoriseringen.
faktoriserar som en produkt av polynom av grad 1 i
K[x]. Ange faktoriseringen.
- 7.
- Bestäm produkten av
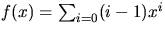 och
och
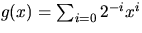 i
i ![$\mathbb Q[[x]].$](img14.gif)
- 8.
- Ringen
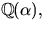 där
där 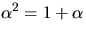 är en kropp.
Bestäm de gemensamma nollställena till polynomen
är en kropp.
Bestäm de gemensamma nollställena till polynomen
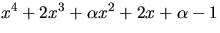 och
och
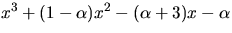 i
i 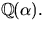
Skrivningen beräknas vara färdigrättad fredagen den 17 april. Den kan
återfås samma dag i mottagningsrummet för matematik i matematiskt
centrum. Mottagningen är öppen kl 12.00-13.00.
Förslag till svar:
4) 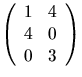 5)
5) 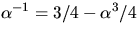 6)
6) 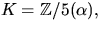 där
där
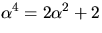 och
och
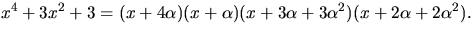
7) 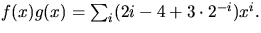 8)
8) 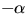 och
och 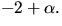



Next: About this document ...
Jan-Alve Svensson
4/30/1998
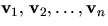 i Km är linjärt oberoende?
i Km är linjärt oberoende?
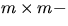 matris med element i kroppen K.
Visa att om
matris med element i kroppen K.
Visa att om 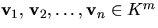 är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
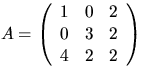 och
och
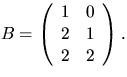
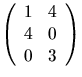 5)
5)