Tentamen i MAN011 Aritmetik och algebra, del 2, 98 05 23.

1.

Formulera och bevisa faktorsatsen för polynom i K[x], där K är en kropp.

2.

Visa att varje polynom av grad 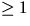$\geq 1$ i K[x], där K är en kropp, kan skrivas som en produkt av irreducibla polynom.

3.

Formulera och bevisa Gauss lemma.

4.

Vilket eller vilka av följande polynom är irreducibla i $\mathbb Q[x]$?

a) x³-3x²+4x-4    b) x⁴+x-3    c) x¹⁵-25x¹³+85x⁷-15x³+1235.

Motivera noggrant!

5.

Bestäm, om möjligt, en inverterbar matris C och en diagonal matris D, så att A=CDC^-1, när

$$A=\left(\begin{array} {rrr} 0&1&1\\ 0&1&1\\ 2&1&2\end{array}\right)$$

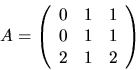
med element i 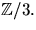$\mathbb Z/3.$

6.

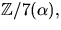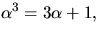Visa att $\mathbb Z/7(\alpha),$ där $\alpha^{3}=3\alpha+1,$ är en kropp och bestäm inversen till $\alpha^{2}+3\alpha+6\in \mathbb Z/7(\alpha)$.

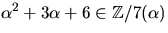7.

Bestäm en så liten kropp K som möjligt, som innehåller 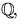$\mathbb Q,$ så att polynomet f(x)=x⁴+8x³+18x²+8x-7 faktoriserar som en produkt av polynom av grad 1 i K[x]. Ange faktoriseringen.

8.

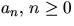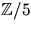Följden $a_{n},\,n\geq 0$ i $\mathbb Z/5$ definieras rekursivt av

$$\begin{array} {l} a_{0}=1,\,a_{1}=1,\,a_{2}=4\\ a_{n}=4a_{n-2}+4a_{n-3},n\geq 3.\end{array}$$

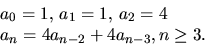
Bestäm följdens period.

Skrivningen beräknas vara färdigrättad fredagen den 29 maj. Den kan återfås samma dag i mottagningsrummet för matematik i matematiskt centrum. Mottagningen är öppen kl 12.00-13.00.

Lösningar finns på kursens hemmsida:

www.math.chalmers/Math/Grundutb/GU/MAN011/V98-2/

efter skrivningstidens slut.
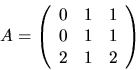
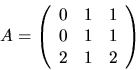