Tentamen i MAN011 Aritmetik och algebra, del 2, 98 08 22.
- 1.
- Formulera och bevisa kinesiska restsatsen för polynom i
![$\mathbb
Q[x]$](img1.gif) . (Fallet med två ekvationer räcker.)
. (Fallet med två ekvationer räcker.)
- 2.
- Låt K vara en kropp. Visa att två polynom
![$f(x),\,g(x)\in K[x]$](img2.gif) har
en största gemensam delare gemensam delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x) för några polynom
har
en största gemensam delare gemensam delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x) för några polynom ![$a(x),\,b(x)\in K[x]$](img3.gif) .
. - 3.
- (a)
- Låt K vara en kropp. Vad menas med att vektorerna
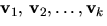 i Kn är linjärt oberoende?
i Kn är linjärt oberoende?
- (b)
- Visa att egenvektorer som hör till olika egenvärden är linjärt
oberoende.
- 4.
- Visa
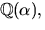 där
där 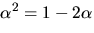 är en kropp och
betsäm inversen till
är en kropp och
betsäm inversen till 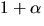 .
. - 5.
- Matrisen B nedan är inverterbar. Lösekvationen AX=B-1, där
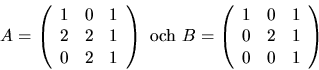
med element i 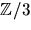 .
. - 6.
- Bestäm produkten av
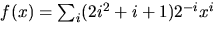 och
och
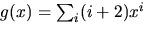 i
i ![$\mathbb Q[[x]]$](img12.gif) .
. - 7.
- Bestäm en så liten kropp K som möjligt, som innehåller
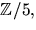 sådan att polynomet x3+x2+1 faktoriserar som en produkt av
polynom av grad 1 i K[x].
sådan att polynomet x3+x2+1 faktoriserar som en produkt av
polynom av grad 1 i K[x].
- 8.
- Följden
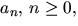 i
i 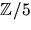 definieras rekursivt av
definieras rekursivt av
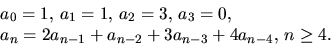
Bestäm följdens period.
Skrivningen beräknas vara färdigrättad fredagen den 28 augusti. Den kan
återfås samma dag i mottagningsrummet för matematik i matematiskt
centrum. Mottagningen är öppen kl 12.00-13.00.
Lösningar finns på kursens hemmsida:
www.math.chalmers/Math/Grundutb/GU/MAN011/V98-2/
efter skrivningstidens slut.
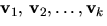 i Kn är linjärt oberoende?
i Kn är linjärt oberoende?
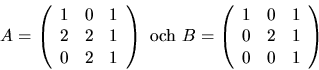
![]()
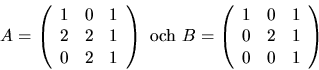
![]()