Tentamen i Aritmetik och algebra, del 2, 98 xx 01.
- 1.
- Formulera och bevisa faktorsatsen för polynom i K[x], där K är en kropp.
- 2.
- Formulera och bevisa kinesiska restsatsen för polynom i
![$\mathbb Q[x].$](img1.gif) (Fallet med två ekvationer räcker.)
(Fallet med två ekvationer räcker.)
- 3.
- (a)
- Låt K vara en kropp.
Vad menas med att vektorerna
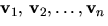 i Km är linjärt oberoende?
i Km är linjärt oberoende?
- (b)
- Låt A vara en
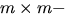 matris med element i kroppen K.
Visa att om
matris med element i kroppen K.
Visa att om 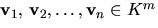 är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
- 4.
- Visa att
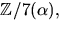 där
där 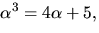 är en kropp
och invertera elementet
är en kropp
och invertera elementet 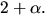
- 5.
- Matriserna A och B har element i
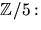
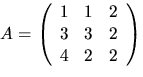 och
och
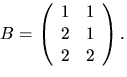
Lös ekvationen AX=B.
- 6.
- Visa att
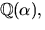 där
där 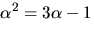 är en kropp
och lös ekvationen
är en kropp
och lös ekvationen
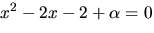 i
i 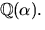
- 7.
- Betäm produkten av
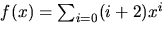 och
och
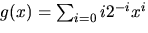
![$\mathbb Q[[x]].$](img17.gif)
- 8.
- Bestäm perioden av följden an i
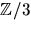 som definieras av
som definieras av
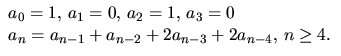
Förslag till svar:
4) 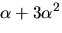 5)
5) 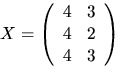 6)
6) 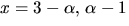 7)
7)  8) 24
8) 24
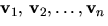 i Km är linjärt oberoende?
i Km är linjärt oberoende?
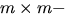 matris med element i kroppen K.
Visa att om
matris med element i kroppen K.
Visa att om 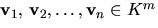 är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
är egenvektorer till A som hör till olika egenvärden, så är
de linjärt oberoende.
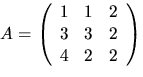 och
och
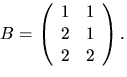
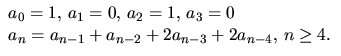
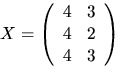 6)
6)