Tentamen i Aritmetik och algebra, del 2, 98 xx 04.
- 1.
- Visa att en formell potensserie
![$f\in K[[x]],$](img1.gif) där K är en kropp är
inverterbar om
där K är en kropp är
inverterbar om 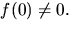
- 2.
- (a)
- Vad menas med ett primitivt polynom?
- (b)
- Formulera och bevisa Gauss lemma.
- 3.
- Låt f vara ett polynom i K[x]. Visa att
![$g\in K[x]/f$](img3.gif) är
inverterbart om och endast om
är
inverterbart om och endast om 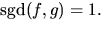
- 4.
- Visa att
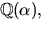 där
där 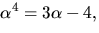 är en kropp
och invertera elementet
är en kropp
och invertera elementet 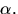
- 5.
- Avgör om vektorerna
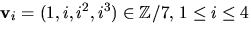 är linjärt oberoende eller ej.
är linjärt oberoende eller ej.
- 6.
- Bestäm inversen till
![$f(x)=2+2x+x^{2}+x^{3}+\cdots
+x^{n}+\cdots\in\mathbb Q[[x]].$](img9.gif)
- 7.
- Bestäm en kropp K som innehåller
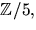 så att
så att ![$x^3+2x+4\in
\mathbb Z/5[x]$](img11.gif) faktoriserar som en produkt av polynom av grad 1 i
K[x]. Ange faktoriseringen.
faktoriserar som en produkt av polynom av grad 1 i
K[x]. Ange faktoriseringen.
- 8.
- Beräkna summan
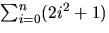 i
i 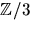
Förslag till svar:
4) 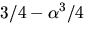 5) Linjärt oberoende
6)
5) Linjärt oberoende
6) 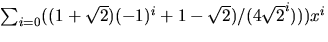 7)
7) 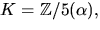 där
där 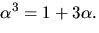
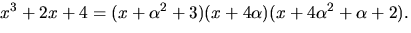 8)
8) 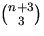
![]() 5) Linjärt oberoende
6)
5) Linjärt oberoende
6) ![]() 7)
7) ![]() där
där ![]()
![]() 8)
8) ![]()