


Next: About this document ...
Tentamen i Aritmetik och algebra, del 2, 98 xx 06.
- 1.
- Formulera och bevisa faktorsatsen för ett polynom i K[x], där K
är en kropp.
- 2.
- Visa att varje polynom
![$f\in K[x],$](img1.gif) där K är en kropp, kan skrivas
som en produkt av irreducibla polynom i K[x].
där K är en kropp, kan skrivas
som en produkt av irreducibla polynom i K[x].
- 3.
- Formulera och bevisa Eisensteins kriterium.
- 4.
- Dela upp
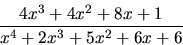
i partial
bråk med rationella koefficienter.
- 5.
- Bestäm, om möjligt, matriser C och D, där D är diagonal, så att
A=CDC-1, och
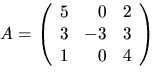
har element i 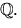
- 6.
- Bestäm inversen till
![$f(x)=\sum_{i=0}a_{i}x^{i}\in \mathbb Z/5[[x]],$](img5.gif) där
där 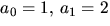 och
och 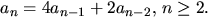
- 7.
- Låt an vara antalet sätt att skriva det icke-negativa heltalet
n som en summa av ett antal av talen
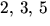 och 7. Ange ett
uttryck för den genererande funktionen och bestäm en
rekursionsekvations som satisfieras av an.
och 7. Ange ett
uttryck för den genererande funktionen och bestäm en
rekursionsekvations som satisfieras av an.
- 8.
- Visa att ringen
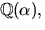 där
där 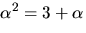 är en
kropp. Lös ekvationen
är en
kropp. Lös ekvationen 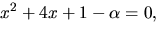 där
där 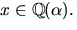
Förslag till svar:
4) 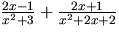
5) 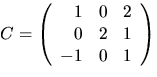 och
och
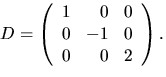
6) 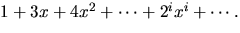
7) 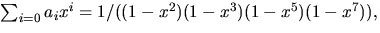 an=an-2+an-3-an-8-an-9+an-14+
an-15-an-17,
an=an-2+an-3-an-8-an-9+an-14+
an-15-an-17,
när 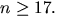
8) 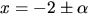
Jan-Alve Svensson
4/30/1998
![]()
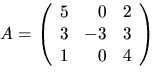
![]()
![]()
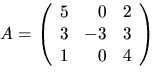
![]()
![]()
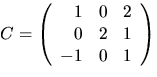 och
och
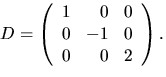
![]()
![]() an=an-2+an-3-an-8-an-9+an-14+
an-15-an-17,
an=an-2+an-3-an-8-an-9+an-14+
an-15-an-17,
![]()
![]()