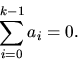Tentamen i MAN011 Aritmetik och algebra, del 2,
99 01 17, kl 8.45-13.45.
- 1.
- (a)
- Definiera vad som menas med en största gemensam delare till två polynom
f(x) och g(x) med koefficienter i kroppen K.
- (b)
- Visa att två polynom
![$f(x),\,g(x)\in K[x]$](img1.gif) har en största gemensam
delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x),
för några polynom
har en största gemensam
delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x),
för några polynom ![$a(x),\,b(x)\in K[x]$](img2.gif) .
.
- 2.
- Formulera och bevisa Eisensteins kriterium för ett primitivt
polynom
![$f(x)\in \mathbb Z[x]$](img3.gif) .
. - 3.
- Låt A vara en
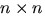 -matris med element i kroppen K. Visa
att om
-matris med element i kroppen K. Visa
att om 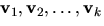 är
egenvektorer till A som hör till olika egenvärden, så är de
linjärt oberoende.
är
egenvektorer till A som hör till olika egenvärden, så är de
linjärt oberoende.
- 4.
- Matrisen A med element i
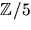 nedan är inverterbar. Visa
detta och lös ekvationen XA=B, där
nedan är inverterbar. Visa
detta och lös ekvationen XA=B, där
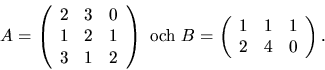
- 5.
- Visa att
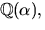 där
där 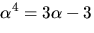 är en kropp
och bestäm inversen till
är en kropp
och bestäm inversen till 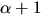 .
. - 6.
- Bestäm en så liten kropp K som möjligt, som innehåller
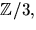 så att
så att ![$x^{4}+2x^{3}+x+1\in
\mathbb Z/3[x]$](img12.gif) faktoriserar som en produkt av polynom av grad 1 i
K[x]. Ange faktoriseringen.
faktoriserar som en produkt av polynom av grad 1 i
K[x]. Ange faktoriseringen.
- 7.
- Talföljden
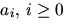 i
i 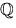 definieras av
definieras av
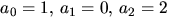 och
ai=9ai-1/2-6ai-2+2ai-3, när
och
ai=9ai-1/2-6ai-2+2ai-3, när 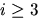 .Beräkna
.Beräkna 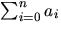 .
. - 8.
- Följden
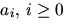 i kroppen K satisfierar den linjära
rekursionsekvationen
i kroppen K satisfierar den linjära
rekursionsekvationen
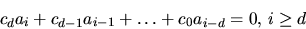
av grad d med koefficienter i K. Man vet att 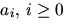 är
periodisk med period k och att
är
periodisk med period k och att 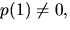 där
där
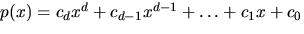 . Visa att
. Visa att
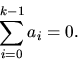
![$f(x),\,g(x)\in K[x]$](img1.gif) har en största gemensam
delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x),
för några polynom
har en största gemensam
delare d(x) och att denna kan skrivas
d(x)=a(x)f(x)+b(x)g(x),
för några polynom ![$a(x),\,b(x)\in K[x]$](img2.gif) .
.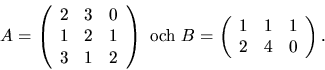
![]()