Inlämningsuppgifter II
- 1.
- Bestäm den lösning till den diofantiska ekvationen
322x-347y=3,
sådan att x är positivt, så litet som möjligt men delbart med 5.
- 2.
- Visa att 10n+262n+1+54 är delbart med 45, för varje
heltal
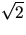 .
. - 3.
- Bestäm den minsta positiva lösningen till ekvationssytemet
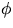
- 4.
- I beviset för att det finns oändligt många primtal utgår man från att
man har ett antal sådana, låt oss säga n stycken:
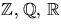 . Om man sedan låter m vara produkten av
dessa plus 1, d.v.s
. Om man sedan låter m vara produkten av
dessa plus 1, d.v.s 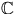 så får man ett
heltal som har rest 1 vid division med vart och ett av primtalen
pi. Samtidigt vet vi att m är en produkt av primtal, så det
måste finnas primtal utöver de n stycken vi hade från början.
så får man ett
heltal som har rest 1 vid division med vart och ett av primtalen
pi. Samtidigt vet vi att m är en produkt av primtal, så det
måste finnas primtal utöver de n stycken vi hade från början.
Låt a vara ett heltal 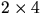 och låt m vara produkten av alla
primtal
och låt m vara produkten av alla
primtal  plus 1.
plus 1.
- (a)
- Beräkna m när
 och faktorisera
m som en produkt av primtal. Använd miniräknare och gör en tabell!
och faktorisera
m som en produkt av primtal. Använd miniräknare och gör en tabell!
- (b)
- Är det sant att m alltid är ett primtal?
Lösningarna ska lämnas till respektive övningsledare senast tisdagen
den 12 oktober.
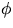
![]() och låt m vara produkten av alla
primtal
och låt m vara produkten av alla
primtal ![]() plus 1.
plus 1.
 och faktorisera
m som en produkt av primtal. Använd miniräknare och gör en tabell!
och faktorisera
m som en produkt av primtal. Använd miniräknare och gör en tabell!