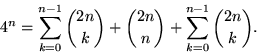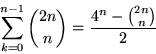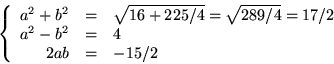
![]()
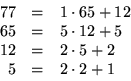
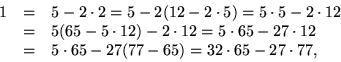
Samtliga lösningar ges nu av
Svar x=-567+65k, y=672-77k, där k är ett godtyckligt heltal.
Vi bestämmer först för vilka n som uttrycket delas av 7, dvs är
kongruent modulo 7. Vi har (Fermats lilla sats ger att
![]() ):
):
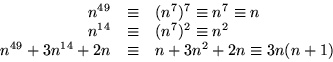
Vi undersöker för vilka värden på n som ![]() . Vi får (Fermats lilla sats ger att
. Vi får (Fermats lilla sats ger att ![]() ):
):
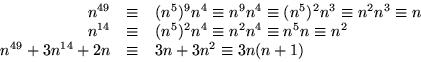
![]()
![]()
Svar: De heltal n som är av formen 35k, 14+35k, 20+35k och 34+35k, där k är ett godtyckligt heltal.
- (a)
- Vi har att
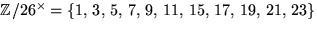 har 12 element,
så en delgrupp har ordning 1, 2, 3, 4, 6 eller 12 enligt
Lagranges sats.
Vi börjar med att undersöka cykliska delgrupper:
har 12 element,
så en delgrupp har ordning 1, 2, 3, 4, 6 eller 12 enligt
Lagranges sats.
Vi börjar med att undersöka cykliska delgrupper:
Vi ser att ordningen av 7 är större än 6, så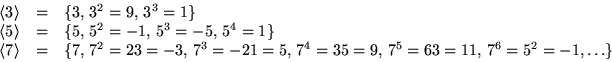
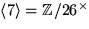 . Gruppen är alltså cyklisk och har
därför precis en delgrupp av ordning d för varje delare d till
12. Den är
. Gruppen är alltså cyklisk och har
därför precis en delgrupp av ordning d för varje delare d till
12. Den är 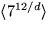 .
.Delgrupperna är alltså
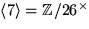
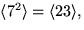
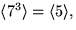
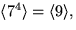
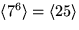 och
och 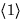 .
. - (b)
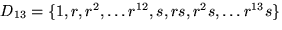 och r13=1=s2 samt sr=r-1s.
och r13=1=s2 samt sr=r-1s.
Eftersom
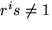 och risris=ri-is2=1 har
elementen s, rs, r2s,
och risris=ri-is2=1 har
elementen s, rs, r2s, 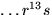 alla ordning 2
resten av gruppen består av
alla ordning 2
resten av gruppen består av 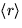 som har ordning 13
och därför inte innehåller något element av ordning 2.
som har ordning 13
och därför inte innehåller något element av ordning 2.
Eftersom D13 har ordning
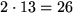 gäller enligt Lagranges
sats att en delgrupp har ordning 1, 2, 13 eller 26.
gäller enligt Lagranges
sats att en delgrupp har ordning 1, 2, 13 eller 26.
En (del)grupp var ordning är ett primtal är cykliska, så en delgrupp av ordning 2 genereras av ett element av ordning 2. Det finns 13 olika sådana:
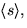
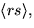
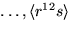 .
.En delgrupp av ordning 13 kan inte innehålla något element av ordning 2, så den enda delgruppen av ordning 13 är
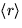 .
.Svar: a)
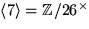
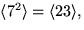
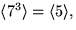
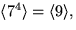
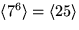 och
och 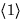
b)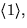
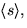
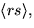
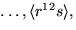
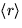 och D13.
och D13.
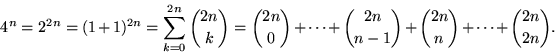
![]()
![]()