Lösningar till tentamen i MAN011, Aritmetik och algebra, del 1, 97 11 01

4.

Vi bestämmer $\mbox{sgd}(36,49)$ med Euklides algoritm:

$$\begin{array} {rcl} 49 &=& 1\cdot 36+13\ 36 &=& 2\cdot 13... ... 1\cdot 10+3\ 10 &=& 3\cdot 3 +1\ 3 &=& 3\cdot 1\end{array}$$

Detta ger $\mbox{sgd}(36,49)=1$. Vi löser ekvationen

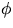
36x+49y=1

med Euklides algrotim baklänges:

$$\begin{array} {rcl} 1&=&10-3\cdot 3=10-3\cdot(13-10)=4\cdot(... ... 13=\ &=&4\cdot 36-11(49-36)=15\cdot 36-11\cdot 49\end{array}$$

Detta ger att $x_{1}=15,\,y_{1}=-11$ löser 36x+49y=1, så $x_{1}=15\cdot 21,\,y_{1}=-11\cdot 21$ löser 36x+49y=21.Vi subtraherar de två likheterna

$$\begin{array} {rcl} 36x+49y&=&21\ 36x_{1}+49y_{1}&=&21\end{array}$$

och får 36(x-x₁)+49(y-y₁)=0, dvs 36(x-x₁)=49(y₁-y). Men 36 och 49 är relativt prima så vi får

$$\begin{array} {rcl} 49\,\vert\,x-x_{1}&\Rightarrow & x=x_{1}+36k\ 36\,\vert\,y-y_{1}& \Rightarrow &y=y_{1}+49l,\end{array}$$

för några heltal k och l. Insättning i 36x+49y=21 ger $36\cdot 49(k+l)=0,$ så l=-k. Lösningarna är alltså

$$\begin{array} {rcl} x=15\cdot 21+k=315+49k\ y=-11\cdot 21-k=-231-36k,\end{array}$$

där $k\in \mathbb Z$ är godtyckligt. Ersätter vi k med -6+k får vi ett hyggligare svar:

$$\begin{array} {rcl} x=315+49(-6+k)=21+49k\ y=-231-36(6-k)=-15-36k.\end{array}$$

Svar: $\left\{\begin{array} {rcl} x&=&21+49k\ y&=&-15-36,\end{array}\right.$ där k är ett godtyckligt heltal.

5.

Att $x\equiv 5\mbox{ mod }25$ ger att x=5+25k, för något heltal k. Insatt i den andra ekvationen ger detta

$$4\equiv x\equiv 5+4k\Rightarrow 4k\equiv -1\mbox{ mod }21.$$

Multiplikation med 5 ger $-k\equiv 20k\equiv -5,$ dvs $k\equiv 5\mbox{ mod }21,$ så k=5+21l, för något heltal l. Detta ger

$$x=5+25k=5+25(5+21l)=130+21\cdot 25l.$$

Insatt i den första ekvationen ger detta

$$3\equiv x\equiv 0+8\cdot (-1)l\Rightarrow 8l\equiv -3\mbox{ mod }13.$$

Multiplikation med 5 ger $l\equiv 40l\equiv -15\equiv -2\equiv 11\mbox{ mod }13,$ så l=11+13m, för $m\in \mathbb Z$.Detta ger

$$x=130+21\cdot 25l=130+21\cdot 25(11+13m)=5905+6825m,$$

där m är ett godtyckligt heltal.

Svar: x=5905+6825m, där m är ett godtyckligt heltal.

6.

$$\begin{array} {rcl} 0&=&z^{2}-(5-3i)z+4-7i=(z-(5-3i)/2)^{2}-... ...5-3i)/2)^{2}-(25-30i-9)/4+4-7i=(z-(5-3i)/2)^{2}+i/2.\end{array}$$

Vi sätter z-(5-3i)/2=a+ib, där $a,\,b\in \mathbb R,$ och får

-i/2=(a+ib)²=a²-b²+2abi

som ger ekvationssystemet

$$\left\{ \begin{array} {rclr} a^{2}+b^{2}&=&1/2&\mbox{ (läng... ...realdel)}\ 2ab&=&-1/2&\mbox{ (imaginärdel)}\end{array}\right.$$

Addition av de två första ekvationerna ger 2a²=1/2, dvs $a=\pm 1/2$. Subtraktion ger 2b²=1/2, så $b=\pm 1/2$. Den tredje ekvationen ger att a och b har olika tecken. Vi får

$$z-(5-3i)/2=a+ib=\pm(1-i)/2\Rightarrow z=(5-3i)/2\pm(1-i)/2= \left\{\begin{array} {rcl} 3-2i\ 2-i\end{array}\right.$$

Svar: $z=\left\{\begin{array} {rcl} 3-2i\ 2-i\end{array}\right.$

7.

Med kvadratkomplettering och konjugatregeln har vi

$$\begin{array} {rcl} x^{4}+4x^{2}-1&=&(x^{2}+2)^{2}-5=(x^{2}... ...}-2})(x-i\sqrt{\sqrt{5}-2}) (x+i\sqrt{\sqrt{5}-2}). \end{array}$$

Detta är faktoriseringen i $\mathbb C[x]$.

För $x\in mathbb R$ är $x^{2}+\sqrt{5}+2\geq \sqrt{5}+2,$ som därför saknar nollställe och är irreducibelt enligt Faktorsatsen, eftersom det har grad 2.

Om x⁴+4x²-1 är en produkt av två polynom i $\mathbb Q[x]$ av grad 2 måste, enligt entydigheten i faktoriseringen i irreducibla polynom, ett av dem vara (associerat med) $x^{2}+2-\sqrt{5}$ och det andra (associerat med) $x^{2}+2+\sqrt{5}.$Men $2+\sqrt{5}$ är nollställe till (x-2)²-5=x²-4x-1, vars ända möjliga rationella nollställen är $\pm 1\not=2+\sqrt{5}$. Alltså är $2-\sqrt{5}\not\in \mathbb Q,$ så x⁴+4x²-1 är inte en produkt av två polynom av grad 2 i $\mathbb Q[x]$.

De möjliga rationella nollställena till x⁴+4x²-1 är $\pm 1,$men inget duger. Enligt Faktorsatsen saknar det faktor av grad 1, och därmed av grad 3, i $\mathbb Q[x]$ Alltså är x⁴+4x²-1 irreducibelt i $\mathbb Q[x]$.

Svar: $\begin{array} {rcl} x^{4}+4x^{2}-1&\mbox{ i }&\mathbb Q[x]\ (x^{2}+2-\sqrt{5}... ...+\sqrt{\sqrt{5}-2})(x-i\sqrt{\sqrt{5}-2})&\mbox{ i }& \mathbb C[x].\end{array}$

8.

Ett ord av längd $k,\,3\leq k\leq 8$ kan delas i tre ord genom att sätta in ett mellanslag på två av mellanrummen mellan bokstäverna, dvs på ${k-1\choose 2}$ olika sätt. Om a_k betecknar antalet ord av längd k blir det sökta antalet meningar

$$\sum_{k=3}^{8}ak{k-1\choose 2}$$

Det återstår att beräkna $a_{k},\,3\leq k\leq 8$.

k=3)
Fall 1) alla bokstäver olika: $4\cdot 3\cdot 2=24$ möjligheter.
Fall 2) två lika bokstäver: välj en av A, B, C, D och sedan två av tre platser. Detta ger $4\cdot{3\choose 2}\cdot 3=36$ möjligheter. Alltså

a₃=24+36=60.

k=4)
Fall 1) två par av bokstäver: välj två bland A, B, C, D och två av fyra platser för det första paret i bokstavsordning. Detta ger ${4\choose 2}{4\choose 2}=36$ möjligheter.
Fall 2) ett par: välj en bland A, B, C, D och två av fyra platser. Placera ut olika på de återstående två platserna. Detta ger $4\cdot{4\choose 2}\cdot3\cdot 2=144$ möjligheter.
Fall 3) alla olika: $4\cdot 3\cdot 2\cdot 1=24$. Alltså

a₄=36+144+24=204.

k=5)
Fall 1) två par: Välj två A, B, C, D och två av fem platser för det första paret i bokstavsordning och två av de återstående tre för den andra. Placera in en bokstav till. Detta ger ${4\choose 2}{5\choose 2}{3\choose 2}2=360$ möjligheter.
Fall 2) ett par: Välj en A, B, C, D och två av fem platser för paret. Placera in olika bokstäver på de återstående tre platserna. Detta ger $4{5\choose 2}3\cdot 2\cdot 1=240$ möjligheter.Alltså

a₅=360+240=600.

k=6)
Fall 1) tre par: Välj tre av A, B, C, D och två av sex platser för det första paret i bokstavsordning och två av de återstående fyra för det andra. Placera in sista paret. Detta ger ${4\choose 3}\cdot{6\choose 2}{4\choose 2}=360$ möjligheter.
Fall 2) två par: Välj två av A, B, C, D och två av sex platser för den första i bokstavsordning och två av de återstående fyra för det andra. Placera in olika bokstäver på de återstående platserna. Detta ger ${4\choose 2}{6\choose 2}{4\choose 2}2\cdot 1=1080$ möjligheter. Alltså

a₆=360+1080=1440.

k=7)
tre par: Välj tre av A, B, C, D och två av sju platser för det första paret i bokstavsordning och två av de återstående fem för det andra och två av de återstående tre för det sista paret. Placera in en bokstav. Detta ger ${4\choose 3}{7\choose 2}{5\choose 2}{3\choose 2}\cdot 1=2520$ möjligheter. Alltså

a₇=2520.

k=8)
fyra par: Välj två platser bland åtta och placera ut första paret i bokstavsordning. Välj sedan två bland de återstående sex för det andra och två bland de återstående fyra för det tredje. Placera in sista paret. Detta ger ${8\choose 2}{6\choose 2}{4\choose 2}1=2520$möjligheter. Alltså

a₈=2520.

Vi har nu att det sökta antalet är

$$\begin{array} {rcl} 60{2\choose 1}+204{3\choose 2}+600{4\cho... ...oose 2}=\ 60+612+3600+14400+37800+52920=\ =109392.\end{array}$$

Svar: 109 392 meningar.