![]()
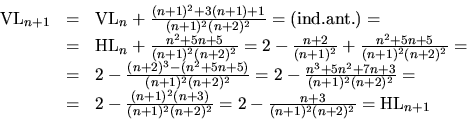
Så påståendet är sant även för n+1. Med induktion är därför
påståendet sant för alla ![]()

(3) ger ![]() . I (1) ger detta
. I (1) ger detta
![]()
![]()
![]()
![]()
![]()
![]()
Svar: Exakt 1557 kronor.
![]()
Modulo 2 gäller
![]()
För att se att 12 delar p(n) när n är jämnt, räcker det att
visa att 3 och 4 delar p(n) för sådana värden på n, ty
![]() och 3 och 4 är relativt prima.
och 3 och 4 är relativt prima.
Vi har redan sett att 3 delar p(n) (för varje värde på n). Det återstår att visa att 4 delar p(2k) för varje heltal k.
Modulo 4 har vi
![]()
- (a)
- G är cylisk om det finns ett element a i G så att
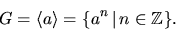
- (b)
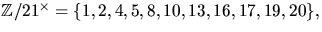 så
så 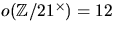 . Vi undersöker om det finns
något element av ordning 12.
. Vi undersöker om det finns
något element av ordning 12.
o(1)=1
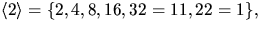 så o(2)=6.
så o(2)=6.
Elementen i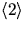 har ordning som delar 6
enligt Lagranges sats. Bara 5,10,13,17,19,20 återstår.
har ordning som delar 6
enligt Lagranges sats. Bara 5,10,13,17,19,20 återstår.
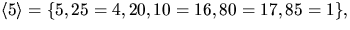 så
o(5)=6.
så
o(5)=6.
Elementen i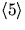 har ordning som delar 6, så
bara 10,13,19 återstår.
har ordning som delar 6, så
bara 10,13,19 återstår.
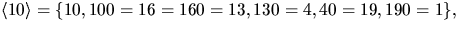 så o(10)=6. Eftersom
så o(10)=6. Eftersom 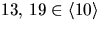 kan de
inte har ordning 12.
kan de
inte har ordning 12.
Alltså har inget element ordning 12 och gruppen är inte cyklisk.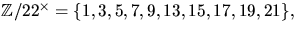 så
så
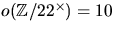 . Vi undersöker om det finns
något element av ordning 10.
. Vi undersöker om det finns
något element av ordning 10.
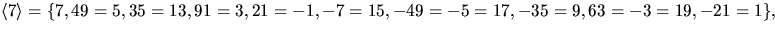 så o(7)=10 och gruppen är cyklisk.
så o(7)=10 och gruppen är cyklisk.
Svar: ![]() är inte cyklisk, men
är inte cyklisk, men
![]() (t.ex.) och är därför
cyklisk.
(t.ex.) och är därför
cyklisk.
8x1+8x2+8x3+40x4=200.
Division med 8 gerx1+x2+x3+5x4=25.
Vi söker heltalslösningar där ![]() och
och
![]() . Låt
. Låt ![]() och
x4=y4+1. Vi får
och
x4=y4+1. Vi får
![]()
![]()
![]()
![]()
Svar: 109 olika kalas.