0=z2-(3-7i)z-10-11i=(z-(3-7i)/2)2-(-40-42i)/4-10-11i= (z-(3-7i)/2)2-i/2.
Vi ska alltså lösa ekvationen (z-(3-7i)/2)2=i/2 och sätter därför z-(3-7i)/2=a+bi, där a och b är reella. Vi får (a+bi)2=i/2 och jämför längd, realdel och imaginär del av de båda leden och får ekvationssystemet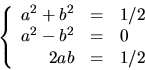
Eftersom a+bi=z-(3-7i)/2 får vi ![]() .
.
Svar: ![]() .
.
![]()
De två nedersta ekvationerna löses alltså av alla x=7+51(16+41k2), där k2 är ett godtyckligt heltal.
Vi sätter in detta uttryck för x i den översta ekvationen och bestämmer k2, så att även denna gäller. Vi får
![]()
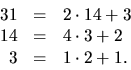
De tre ekvationerna löses alltså av
![]()
Svar: 21 733.
![]()
![]()
![]()
![]()
Svar: ![]() (vardera med
multiplicitet 2).
(vardera med
multiplicitet 2).
- (a)
- Gruppen består av elementen
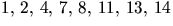 och har ordning 8. Vi
bestämmer ordningen för vart och ett av elementen.
och har ordning 8. Vi
bestämmer ordningen för vart och ett av elementen.
Potenser av 2:
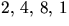 . Ordningen av 2 är 4. Övriga
potenser av 2 har ordning som delar 4 enligt Lagranges sats.
Potenser av 7:
. Ordningen av 2 är 4. Övriga
potenser av 2 har ordning som delar 4 enligt Lagranges sats.
Potenser av 7: 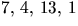 . Ordningen av 7 är 4. Övriga
potenser av 7 har ordning som delar 4.
Potenser av 11:
. Ordningen av 7 är 4. Övriga
potenser av 7 har ordning som delar 4.
Potenser av 11: 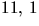 . Ordningen av 11 är 2.
. Ordningen av 11 är 2.
Gruppen har ordning 8, men saknar element av denna ordning. Alltså är gruppen inte cyklisk.
- (b)
- Gruppen består av elementen
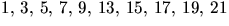 och har alltså
ordning 10. Vi undersöker om den har ett element av denna
ordning.
och har alltså
ordning 10. Vi undersöker om den har ett element av denna
ordning.
Potenser av 3:
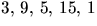 . Ordningen av 3 är
5. Övriga potenser av 3 har ordning som delar 5.
Potenser av 7:
. Ordningen av 3 är
5. Övriga potenser av 3 har ordning som delar 5.
Potenser av 7: 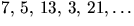 . Vi ser att
ordningen av 7 är >5, samtidigt som den delar gruppens ordning
som är 10. Alltså har 7 ordning 10 och gruppen är cyklisk
med 7 som generator.
. Vi ser att
ordningen av 7 är >5, samtidigt som den delar gruppens ordning
som är 10. Alltså har 7 ordning 10 och gruppen är cyklisk
med 7 som generator.
- (c)
- En cyklisk grupp är kommutativ, men det är inte
D7. T.ex. är
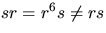 . Alltså är gruppen inte
cyklisk.
. Alltså är gruppen inte
cyklisk.
- (d)
- Kompositionsregeln är addition modulo 211. Varje element är
en multipel av 1, som alltså är en generator. Gruppen är cyklisk
med 1 som generator.
![]()
Bland dessa finns ![]() där tre av variablerna är
där tre av variablerna är ![]() .
.
Vi undersöker hur många lösningar det finns med precis två variabler
![]() . Vi kan välja de två variablerna xi och xj på
. Vi kan välja de två variablerna xi och xj på
![]() sätt. Vi ersätter dessa med zi+8 och zj+8
och döper om de övriga med ``z''. Vi får då ekvationen
sätt. Vi ersätter dessa med zi+8 och zj+8
och döper om de övriga med ``z''. Vi får då ekvationen
z1+z2+z3+z4+z5=8,
som har
Bland dessa finns även lösningar till den ursprungliga
ekvationen med tre variabler ![]() medräknade. De har i själva
verket räknats tre gånger eftersom det finns
medräknade. De har i själva
verket räknats tre gånger eftersom det finns ![]() sätt
att välja 2 bland 3.
sätt
att välja 2 bland 3.
Antalet lösningar med precis två variabler ![]() i den
ursprungliga ekvationen är alltså
i den
ursprungliga ekvationen är alltså
![]()
Vi undersöker nu hur många lösningar den ursprungliga ekvationen har
där precis en av variablerna är ![]() . Variabeln xi kan väljas på 5
sätt. Sedan sätter vi xi=zi+8 och ersätter övriga variabler
med ``z''. Vi får
. Variabeln xi kan väljas på 5
sätt. Sedan sätter vi xi=zi+8 och ersätter övriga variabler
med ``z''. Vi får
z1+z2+z3+z4+z5=16,
som har
Bland dessa finns lösningar till den ursprungliga ekvationen med två
och tre variabler ![]() . De förra har räknats 2 gånger (eftersom
det finns 2 sätt att välja 1 bland 2) och de senare 3
gånger.
. De förra har räknats 2 gånger (eftersom
det finns 2 sätt att välja 1 bland 2) och de senare 3
gånger.
Antalet lösningar till den ursprungliga ekvationen med precis en
variabel ![]() är alltså
är alltså
![]()
Anatalet lösningar till den ursprungliga ekvationen med en, två eller
tre variabler ![]() är alltså
är alltså
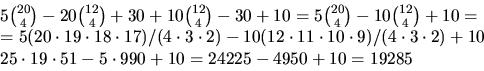
20475-19285=1190
Svar: 1190.