När n=0 är påståendet 2<33/5, vilket är sant.
När n=1 är påståendet -1<34/5, vilket också stämmer.
Antag nu att ![]() och att påståendet gäller när
n<p. Påståendet som ska visas är ap<3p+3/5.
och att påståendet gäller när
n<p. Påståendet som ska visas är ap<3p+3/5.
Enligt indukutionsantagandet har vi ap-1<3p+2/5 och ap-2=3p+1/5. Tillsammans med ap=ap-1+6ap-2 ger detta nu
![]()
Enligt induktionsprincipen gäller nu att an<3n+3/5, för alla
heltal ![]() .
.
![]()
z2-(1+i)z+(10+11i)=(z-(1+i)/2)2-i/2+10+11i,
så vi ska lösa ekvationen (z-(1+i)/2)=-10-21i/2. Vi sätter nu z-(1+i)/2=a+bi, där a och b är rella. Vi utvecklar (a+bi)2 och får a2-b2+2abi och jämför sedan längd, realdel och imaginär del med motsvarande för -10-21i/2. Detta ger ekvationssystemet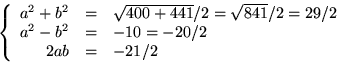
![]()
Svar: ![]() .
.
![]()
![]()
![]()
![]()
![]()
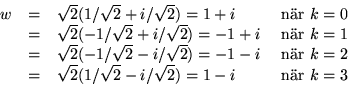
Svar: ![]() .
.
![]()
![]() .(*)
.(*)
Bortser vi från villkoret att variablerna ska var ![]() har
ekvationen
har
ekvationen
![]() (**)
(**)
som har ![]() lösningar. Vi försöker nu reda ut hur
många av dessa som inte är giltiga. De som inte är giltiga är de där
en eller flera varibler antar värden
lösningar. Vi försöker nu reda ut hur
många av dessa som inte är giltiga. De som inte är giltiga är de där
en eller flera varibler antar värden ![]() . Vi ser att högst två
av variablerna kan vara
. Vi ser att högst två
av variablerna kan vara ![]() eftersom summan ska vara 14.
eftersom summan ska vara 14.
Antalet lösningar där minst en variabel är ![]()
Vi väljer en av de sex variablerna (sex möjligheter) och stipulerar
att denna ska vara ![]() . Vi gör sedan samma trick som ovan med
variabelbyte och får att vi sedan ska bestämma antalet
heltalslösningar till
. Vi gör sedan samma trick som ovan med
variabelbyte och får att vi sedan ska bestämma antalet
heltalslösningar till
z1+z2+z3+z4+z5+z6=14-5=9.
Detta antal är
Vi får ![]() . Nu ger inte detta det korrekta antalet
eftersom det bland dessa ingår fall där två variabler är
. Nu ger inte detta det korrekta antalet
eftersom det bland dessa ingår fall där två variabler är ![]() och dessa har räknats två gånger (dels fallet där den första
variabeln är
och dessa har räknats två gånger (dels fallet där den första
variabeln är ![]() dels fallet där den andra är det). Vi ska
därför dra bort de fall där två av variablerna är
dels fallet där den andra är det). Vi ska
därför dra bort de fall där två av variablerna är ![]() . Antalet
sätt att välja två av variablerna är
. Antalet
sätt att välja två av variablerna är ![]() . Samma trick med
variabelbyte som tidigare ger att vi sedan ska bestämma antalet
heltalslösningar till
. Samma trick med
variabelbyte som tidigare ger att vi sedan ska bestämma antalet
heltalslösningar till
z1+z2+z3+z4+z5+z6=9-5=4,
Detta antal är
Antalet ogiltiga lösningar till (*) är alltså ![]() .
.
Antalet lösningar till (**) är därför
![]()
Svar: 1506.