322x-347y=1
genom att använda Euklides algoritm: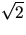
![]()
![]()
Svar: x=680 och y=631.
Vi räknar först modulo 5 och får
![]()
Vi räknar sedan modulo 9 och får
![]()
Detta ger nu att ![]() delar uttrycket, eftersom 5 och 9
har 1 som största gemensam delare.
delar uttrycket, eftersom 5 och 9
har 1 som största gemensam delare.
![]()
![]()
Vi får alltså att ![]() där k2 är
godtyckligt löser ekvationssystemet.
där k2 är
godtyckligt löser ekvationssystemet.
Den minsta positiva lösningen får vi om vi väljer k2=1 och då
blir ![]() .
.
Svar: 29641.
- (a)
- Vi gör en tabell:
n primtal <n produkten av dessa m faktorisering 2 2 2 3 3 3 2, 3 6 7 7 4 2, 3 6 7 7 5 2, 3, 5 30 31 31 6 2, 3, 5 30 31 31 7 2, 3, 5, 7 210 211 211 8 2, 3, 5, 7 210 211 211 9 2, 3, 5, 7 210 211 211 10 2, 3, 5, 7 210 211 211 11 2, 3, 5, 7, 11 2310 2311 2311 12 2, 3, 5, 7, 11 2310 2311 2311 13 2, 3, 5, 7, 11, 13 30030 30031 
- (b)
- Nej! När n=13 är
 .
.