Förslag till lösning av Inlämningsuppgifter III

1.

Gruppen D₁₀ har ordning 20. Enligt Lagranges sats har en delgrupp ordning som delar 20. Detta kan användas för att avslöja mängder som inte är delgrupper. I gruppen D₁₀ gäller att r¹⁰=1 och att srⁱ=r^10-is.

(a)

Mängden innehåller 8 element och kan inte vara en delgrupp, eftersom $8\not\vert\,20$.

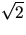(b)

Vi gör en tabell

1 r⁵ s r⁵s

1 1 r⁵ s r⁵s

r⁵ r⁵ 1 r⁵s s

s s r⁵s 1 r⁵

r⁵s r⁵s s r⁵ 1

Vi ser att produkter inte leder utanför mängden och att varje element i mängden har en invers som ligger i mängden (för identitetselementet förekommer på varje rad). Mängden är alltså en delgrupp.

(c)

Mängden är 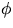$\langle r^{2}\rangle$ och därför en delgrupp.

(d)

Produkten av r⁴ och s, som båda tillhör mängden, är r⁴s, som inte tillhör mängden. Alltså ingen delgrupp.

(e)

Vi gör en tabell:

1 rs

1 1 rs

rs rs 1

Produkter leder inte utanför mängden och varje element har en invers i mängden, så den är en delgrupp.

2.

En grupp G är cyklisk med g som generator om g har samma ordning som gruppen G.

(a)

Gruppen, som består av elementen 1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20, har ordning 12. Vi undersöker om den har ett element av ordning 12.

Potenser av 2: 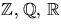$2,\,4,\,8,\,16,\,11,\,1$. Ordningen av 2 är 6. Övriga potenser av 2 har ordning som delar 6.

Potenser av 5: 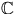$5,\,4,\,20,\,16,\,17,\,1$. Ordningen av 5 är 6. Övriga potenser av 5 har ordning som delat 6.

Potenser av 10: 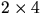$10,\, 16,\, 13,\,4,\,19,\,1.$ Ordningen av 10 är 6. Övriga potenser av 10 har ordning som delar 6.

Vi har sett att gruppen saknar element av ordning 20 och den är därför inte cyklisk.

(b)

Gruppen består av elementen 1, 5, 7, 11 och har ordning 4.

Potenser av 5: $5,\,1,$ så 5 har ordning 2.

Potenser av 7: $7,\,1,$ så 7 har ordning 2.

Potenser av 11: $11,\,1,$ så 11 har ordning 2.

Gruppen saknar element av ordning 4 och är därför inte cyklisk.

(c)

Gruppen består av elementen $0,\,1,\,2,\ldots 210$ med addition modulo 211 som operation. Multipler av 1 ger varje element i gruppen, så gruppen är cyklisk med 1 som generator

(d)

En cyklisk grupp är kommutativ, men S₄ är inte det. T.ex.

$$(1,2)(2,3)=(1,2,3)\mbox{ men }(2,3)(1,2)=(1,3,2).$$

Gruppen är alltså inte cyklisk.

(e)

Gruppen består av elementen 1, 3, 5, 9, 11, 13 och har ordning 6.

Potenser av 3: $3,\,9,\,13,\,11,\,5,\,1$. Vi ser att 3 har samma ordning som gruppen, som därför är cyklisk med 3 som generator.

3.

Eftersom f har reella koefficienter är också $\overline{i-2}=-i-2$ ett nollställe till f. Alltså är f delbart med

(x+2+i)(x+2-i)=(x+2)²+1=x²+4x+5

Utför vi divisionen får vi

f(x)=(x²+4x+5)(6x²-5x+1)

Det återstår att bestämma nollställen till 6x²-5x+1= 6(x²-5x/6+1/6)=
6((x-5/12)²-(1/12)² =6(x-5/12-1/12)(x-5/12+1/12) =6(x-1/2)(x-1/3). Som alltså har nollställena 1/2 och 1/3.

Svar: $-2\pm i,$ 1/2 och 1/3.

4.

De möjliga rationella nollställena är c/d, där $c\,\vert\,-7$ och $d\,\vert\,2,$ d.v.s $c/d=\pm 1/2,\,\pm 1,\, \pm 7/2$ och $\pm 7$. Prövning visar att f(2)=0, så att x-1/2 delar f, enligt faktorsatsen. Men då delar även 2(x-1/2)=2x-1 polynomet. Divisionen ger

f(x)=(2x-1)(x⁴-6x²+7)

För att bestämma nollställena till x⁴-6x²+7 kan vi t.ex. först göra substitutionen t=x² och får då t²-6t+7, som med hjälp av formel har nollställen $t=3\pm\sqrt{2},$ så att x⁴-6x²+7 har nollställena $\pm\sqrt{3+\sqrt{2}}$ och $\pm\sqrt{3-\sqrt{2}}.$

Alternativt kan vi göra en kvadratkomplettering och använda konjugatregeln:

$$x^{4}-6x^{2}+7=(x^{2}-3)^{2}-2=(x^{2}-3)^{2}-\sqrt{2}^{2}= (x^{2}-3-\sqrt{2})(x^{2}-3+\sqrt{2}),$$

där den första faktorn har nollställena $\pm\sqrt{3+\sqrt{2}},$ medan den andra har nollställena $\pm \sqrt{3-\sqrt{2}}$.

Svar: $1/2,\,\pm\sqrt{3+\sqrt{2}}$ och $\pm \sqrt{3-\sqrt{2}}$.