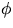Tentamen i MAN011 Aritmetik och algebra, del 1, 00 01 03, kl 8.45-13.45

1.

Formulera och bevisa kinesiska restsatsen. (Fallet med två ekvationer räcker.)

2.

Formulera och bevisa faktorsatsen för polynom med rationella koefficienter.

3.

(a)

Hur lyder definitionen av en största gemensam delare till två polynom f(x) och g(x) med rationella koefficienter?

(b)

Visa att två sådana polynom alltid har en största gemensam delare och att den kan skrivas som en kombination av dem (Bezouts identitet).

4.

Lös ekvationen 0=z²+(1-i)z-4+7i.

5.

Lös den diofantiska ekvationen 77x+65y=21.

6.

För vilka heltal n gäller det att 35 delar n⁴⁹+3n¹⁴+2n?

7.

Bestäm samtliga delgrupper till

(a)

$\mathbb Z/26^{\times}$,

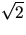(b)

D₁₃.

8.

Visa att

$$\sum_{k=0}^{n-1}{2n \choose k}=\frac{4^{n}-{2n \choose n}}{2},$$

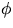
för alla heltal 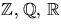$n\geq 1$.

Skrivningarna beräknas vara färdigrättade fredagen den 14 januari. I så fall kan de återfås på mottagningen för matematik i matematiskt centrum fr.o.m denna dag. Mottagningen har öppet måndag till fredag kl 12.30-13.00.
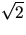