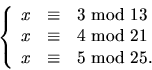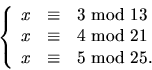Tentamen i Aritmetik och Algebra del 1, 5p, 97 11 01.
- 1.
- (a)
- Visa att om p är ett irreducibelt polynom i
![$\mathbb
Q[x]$](img1.gif) och
och 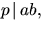 där a och b är polynom med
rationella koefficienter, så gäller att
där a och b är polynom med
rationella koefficienter, så gäller att 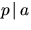 eller
eller
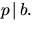
- (b)
- Ge exempel på ett polynom i
![$\mathbb
Q[x]$](img1.gif) som är
irreducibelt i
som är
irreducibelt i ![$\mathbb Q[x],$](img5.gif) men inte i
men inte i ![$\mathbb R[x]$](img6.gif) .
.
- 2.
- Låt
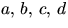 vara heltal och n ett positivt
heltal. Visa att om
vara heltal och n ett positivt
heltal. Visa att om 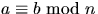 och
och 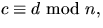 så gäller att
så gäller att 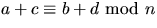 och att
och att
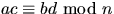 .
. - 3.
- Formulera och bevisa Lagranges sats om ordningen för en delgrupp
till en ändlig grupp.
- 4.
- Bestäm alla lösningar till den diofantiska ekvationen
36x+49y=21.
- 5.
- Bestäm alla heltal x sådana att
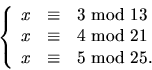
- 6.
- Lös ekvationen z2-(5-3i)z+4-7i=0.
- 7.
- Faktorisera polynomet x4+4x2-1 med hjälp av irreducibla
polynom i
![$\mathbb Q[x],\,\mathbb R[x],$](img13.gif) samt
samt ![$\mathbb C[x]$](img14.gif) .
. - 8.
- Man har två stycken A:n, B:n, C:n och D:n. Hur många olika
``meningar'' med tre ``ord'' kan bildas med dessa bokstäver? (Ett
``ord'' är en sekvens av bokstäver med minst en bokstav.
En ``mening'' är en sekvens av ord.)
Skrivingen beräknas vara färdigrättad fredagen den 14 novembewr. Den
kan återfårs i rasten på föreläsningen i Aritmetik och Algebra del 2
samma dag. Efter det kan skrivningarna hämtas på expeditionen för
matematik i Matematiskt centrum.
![$\mathbb
Q[x]$](img1.gif) och
och 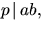 där a och b är polynom med
rationella koefficienter, så gäller att
där a och b är polynom med
rationella koefficienter, så gäller att 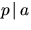 eller
eller
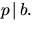
![$\mathbb
Q[x]$](img1.gif) som är
irreducibelt i
som är
irreducibelt i ![$\mathbb Q[x],$](img5.gif) men inte i
men inte i ![$\mathbb R[x]$](img6.gif) .
.