Tentamen i MAN011 Aritmetik och Algebra del 1, 5p, 97-xx-xx.

1.

Formulera och bevisa kinesiska restsatsen (två ekvationer).

2.

Formulera och bevisa triangelolikheten för komplexa tal.

3.

Visa att en delgrupp till en cyklisk grupp är cyklisk.

4.

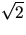
Bestäm ordningen av $5\in\mathbb Z/32^{\times}.$

5.

Bevisa att

$$\sum_{k=0}^{n}\frac{k+1}{(k^2+k+1)(k^2+3k+3)}= \frac{1}{2}\left(1-\frac{1}{(n+1)(n+2)+1}\right)$$

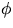
för alla heltal 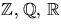$n\geq 0$.

6.

Ekvationen

z³-(4-3i)z²+(2-8i)z+2+4i=0

har en multipel rot. Lös ekvationen!

7.

Kajsa och Kalle tänker flytta ihop och finner att de behöver en bokhylla. De beger sig till ett möbelvaruhus som säljer en bokhylleserie med fyra olika typer av sektioner i tre olika färger. Dessa kan placeras vid sidan av eller ovan på varandra.

Kajsas och Kalles pengar räcker till nio sektioner. De vill att alla sektionerna ska vara olika. Hur många olika bokhyllor (som hänger ihop) har de att välja mellan?

8.

Visa att talet

$$\frac{5^{n-1}}{24}-\frac{4^{n-2}2}{3}+\frac{3^{n-1}}{4}- \frac{2^{n-2}}{3}+\frac{1}{24}$$

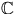
är ett heltal för alla heltal 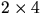$n\geq 1$.