Tentamen i Aritmetik och Algebra del 1, 5p, 98 01 05.

1.

Formulera och bevisa kinesiska restsatsen för heltal. (Fallet med två ekvationer räcker.)

2.

(a)

Formulera och bevis en sats om eventuella rationella nollställen till ett polynom i $\mathbb Z[x]$.

(b)

Visa att 3^1/3 är irrationellt.

3.

Formulera och bevisa triangelolikheten för komplexa tal.

4.

Lös ekvationen z²-5z+3iz+4-8i=0.

5.

Hur många positiva heltalslösningar har ekvationen

x+y+z=91,

där 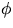$x\geq 10$ och $y\geq 13$?

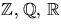6.

Faktorisera polynomet x⁶-3x⁴-9x²-5 med hjälp av irreducibla polynom i $\mathbb Q[x],\,\mathbb R[x]$ och $\mathbb C[x]$.

7.

Hur många delgrupper av ordning $2,\,3,\,5$ och 9 har gruppen D₉?

8.

Undersök om det finns några positiva heltal n, så att

$$\frac{5^{n}-1}{4^{n}-1}$$

är ett heltal. Eventuella slutsatser ska bevisas för full poäng.