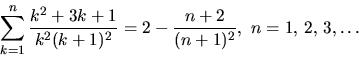Tentamen i MAN011 Aritmetik och Algebra del 1, 5p, 98 03 14.
- 1.
- Formulera och bevisa faktorsatsen.
- 2.
- Visa att om p är ett primtal och
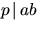 där a och b
är heltal så gäller att
där a och b
är heltal så gäller att 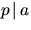 eller
eller 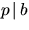 .
. - 3.
- Bevisa Lagranges sats om ordningen för en delgrupp till en ändlig
grupp.
- 4.
- Visa att
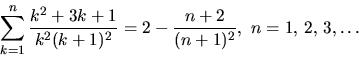
- 5.
- Ungefär 1.500 enkronor staplas på ett bord. När kronorna läggs i
staplar med 10 kronor i varje blir det 7 stycken över, när staplarna
innehåller 7 enkronor var blir det 3 kronor över och när staplarna
består av 13 kronor blir det 10 över. Exakt hur många enkronor låg
det på bordet?
- 6.
- Visa att n3+3n2+14n-12 är delbart med 6 för alla
heltal n och med 12 om n är ett jämnt heltal.
- 7.
- (a)
- Vad menas med att en grupp är cyklisk?
- (b)
- Är grupperna
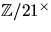 och
och 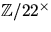 cykliska? Bestäm i så fall en generator för
gruppen.
cykliska? Bestäm i så fall en generator för
gruppen.
- 8.
- Hasse skall köpa kaffebröd till sitt födelsedagskalas. Han
tänker köpa tre olika sorters wienerbröd som alla kostar 8 kronor
styck och en sorts tårta som kostar 40 kronor styck. På hur många
sätt kan han göra detta om han skall köpa minst 3 wienerbröd av
varje sort och minst en tårta och hela kalaset skall kosta 200 kronor?
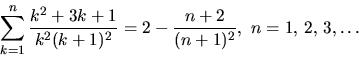
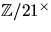 och
och 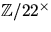 cykliska? Bestäm i så fall en generator för
gruppen.
cykliska? Bestäm i så fall en generator för
gruppen.