Tentamen i MAN011 Aritmetik och algebra, del 1,
98 08 15
- 1.
- Formulera och bevisa triangelolikheten för komplexa tal.
- 2.
- Låt a, b, c, och d vara heltal och n ett positivt
heltal. Visa att om
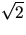 och
och 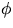 , så gäller att
, så gäller att 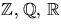 och
och
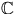 .
. - 3.
- Bevisa Lagranges sats om ordningen för en delgrupp till en ändlig grupp.
- 4.
- Lös ekvationen
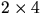
- 5.
- Talföljden
 definieras genom
definieras genom

- (a)
- Ange en formel för an.
- (b)
- Bevisa ditt påstående i (a).
- 6.
- Hur många heltalslösningar har ekvationen x+y+z=51
om
(a)  ,
,  och
och  ,
,
(b)  ,
,  och
och  ?
?
- 7.
- Vilken eller vilka av följande delmängder till S5 är delgrupper?
- (a)
- {(1), (1,2,3,5,4), (1,3,4,2,5), (1,2,5,3,4,) (1,4,5,3,2), (1,4,3,5,2), (1,5,2,4,3)}
- (b)
- {(1), (4,5), (1,2,3), (1,3,2), (1,2,3)(4,5), (1,3,2)(4,5)}
- (c)
- {(1), (1,2,3,5,4), (1,3,4,2,5), (1,4,5,3,2), (1,4,3,5,2), (1,5,2,4,3)}
Motivera dina svar!
- 8.
- Visa att 710n+1+611n-1 är delbart med 43 för varje positivt
heltal n.
![]()
![]()