Tentamen i MAN011 Aritmetik och algebra, del 1,
98 10 30, kl 8.45-13.45
- 1.
- Låt a, b, c, och d vara heltal och n ett positivt
heltal. Visa att om
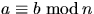 och
och 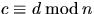 , så gäller att
, så gäller att 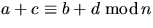 och
och
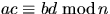 .
.
- 2.
- Formulera och bevisa kinesiska restsatsen. Fallet med två
ekvationer räcker.
- 3.
- (a)
- Formulera och bevisa en sats om eventuella rationella nollställen till
ett polynom med heltalskoefficienter.
- (b)
- Visa att
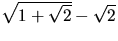 är irrationellt.
är irrationellt.
- 4.
- En talföljd
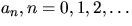 definieras rekursivt av
definieras rekursivt av
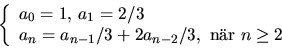
Visa att an<(1/5)(2/3)n+1 för alla heltal 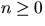 .
. - 5.
- Lös ekvationen
z2-(5-i)z+8-i=0.
- 6.
- Bestäm det minsta positiva heltalet x sådant att
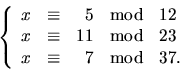
- 7.
- Bestäm alla delgrupper till
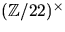 .
. - 8.
- Hur många n-siffriga med siffrorna
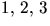 och 4 har ett jämnt
antal 1:or och ett udda antal 2:or?
och 4 har ett jämnt
antal 1:or och ett udda antal 2:or?
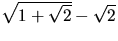 är irrationellt.
är irrationellt.
![]()
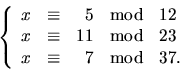
![]()