Tentamen i MAN011 Aritmetik och algebra, del 1,
99 10 30, kl 8.45-13.45
- 1.
- Låt
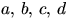 vara heltal och n ett positivt
heltal. Visa att om
vara heltal och n ett positivt
heltal. Visa att om 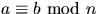 och
och 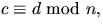 så gäller att
så gäller att 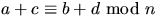 och att
och att
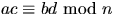 .
. - 2.
- (a)
- Formulera och bevis en sats om eventuella rationella
nollställen till ett polynom i
![$\mathbb Z[x]$](img6.gif) .
.
- (b)
- Visa att 71/7 är irrationellt.
- 3.
- Visa att en delgrupp till en cyklisk grupp är cyklisk.
- 4.
- Lös ekvationen z2-(3-7i)z-10-11i=0.
- 5.
- Bestäm det minsta positiva heltalet som löser ekvationssystemet
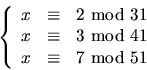
- 6.
- Polynomet f(x)=x4-8x3+18x2-8x+1 har ett multipelt
nollställe. Bestäm alla (komplexa) nollställen till f(x).
- 7.
- Vilken eller vilka av följande grupper är cykliska. Bestäm en
generator i förekommande fall:
- (a)
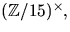
- (b)
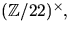
- (c)
- D7,
- (d)
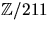 .
.
Motivera noggrant!
- 8.
- Bestäm antalet heltalslösningar till ekvationen
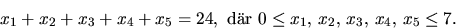
Efter skrivningstidens slut finns förslag till lösningar på kursens
hemsida:
http://www.math.chalmers.se/Math/Grundutb/GU/MAN011/H99-1
Skrivingarna beräknas vara färdigrättade fredgen den 12 november.
![$\mathbb Z[x]$](img6.gif) .
.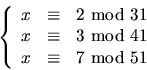
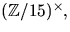
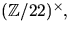
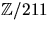 .
. ![]()
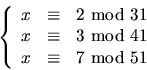
![]()