Inlämningsuppgifter II
- 1.
- Skriv följande polynom som en produkt av irreducibla polynom i
![$\mathbb Z/5[x]:$](img1.gif)
- (a)
- x4+4x3+2x2+3x+4,
- (b)
- x4+x3+4x2+2x+4.
- 2.
- Avgör om
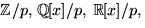 där
där 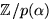 är en
kropp. Avgör också om
är en
kropp. Avgör också om 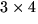 är
inverterbart. Bestäm i så fall inversen.
är
inverterbart. Bestäm i så fall inversen.
- 3.
- Bestäm en så liten kropp K som möjligt som innehåller
 så att f(x)= x4+2x3+4x2+4x+4 faktoriserar som
en produkt av polynom av grad 1 i K[x]. Ange faktoriseringen.
så att f(x)= x4+2x3+4x2+4x+4 faktoriserar som
en produkt av polynom av grad 1 i K[x]. Ange faktoriseringen.
- 4.
- Bestäm en så liten kropp K som möjligt som innehåller
 så att
så att ![$f(x)= x^4+3x^2+2x+2\in \mathbb Z/7[x]$](img7.gif) faktoriserar
som en produkt av polynom av grad 1 i K[x]. Ange
faktoriseringen.
faktoriserar
som en produkt av polynom av grad 1 i K[x]. Ange
faktoriseringen.
Lösningarna ska lämnas till respektive övningsledare senast tisdagen
den 7 december.