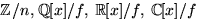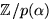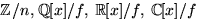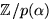Inlämningsuppgifter III
- 1.
- Bestäm en bas för lösningsrummet till ekvationssystemet
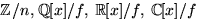
som har koefficienter i 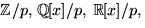 . Hur många lösningar har
ekvationssystemet?
. Hur många lösningar har
ekvationssystemet?
- 2.
- Visa att matrisen
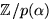
med element i 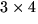 är inverterbar och lös ekvationen
AXA-1=B, där
är inverterbar och lös ekvationen
AXA-1=B, där

- 3.
- Bestäm, om möjligt, en diagonal matris D och en inverterbar C
så att A=CDC-1, när

med element i  .
. - 4.
- Beräkna summan

i  .
.
Lösningarna ska lämnas till respektive övningsledare senast tisdagen
den 21 december.