För att invertera använder vi Euklides algoritm och får
![]() .
.
I
![]() ger detta
ger detta
![]() eller
eller
![]() . Division med
. Division med ![]() ger
nu
ger
nu
![]() så inversen till
så inversen till
![]() är
är
![]() .
.
Svar: Inversen är
![]() .
.
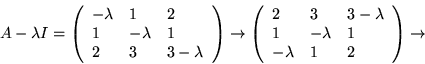
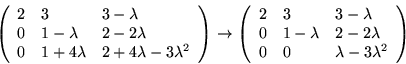
Vi ser att rangen av ![]() är
är ![]() när
när ![]() och när
och när
![]() . Egenvärdena är alltså
. Egenvärdena är alltså
![]() och
och ![]() .
.
Vi söker en egenvektor hörande till vart och ett av dem:
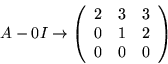
Vi ser att
![]() har lösningen
har lösningen
![]() (t.ex.).
(t.ex.).
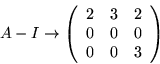
Vi ser att
![]() har lösningen
har lösningen
![]() (t.ex.).
(t.ex.).
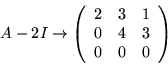
Vi ser att
![]() har lösningen
har lösningen
![]() (t.ex.).
(t.ex.).
Sätter vi nu
![]() vet
vi att
vet
vi att ![]() är inverterbar, eftersom egenvärdena är olika. Sätter vi
är inverterbar, eftersom egenvärdena är olika. Sätter vi
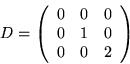
har vi att ![]() och
och ![]() .
.
Svar:
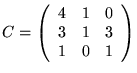 och
och
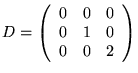
Vi undersöker om ![]() är produkt av två polynom av grad 2 genom att
ansätta
är produkt av två polynom av grad 2 genom att
ansätta
![]() , där vi kan förutsätta att
, där vi kan förutsätta att
![]() och att
och att ![]()
![]()
![]() och
och ![]() är heltal, eftersom polynomet
är primitivt. Identifiering av koefficienter ger ekvationssystemet
är heltal, eftersom polynomet
är primitivt. Identifiering av koefficienter ger ekvationssystemet
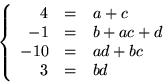
Den nedersta ekvationen ger alternativen ![]()
![]() och
och ![]()
![]() .
.
Det första av dessa ger ![]() i den tredje ekvationen. Adderar
vi den första får vi
i den tredje ekvationen. Adderar
vi den första får vi ![]() eller
eller ![]() . Detta ger
. Detta ger ![]() i den
första och vi ser att dessa värden även löser den andera. Vi har
alltså
i den
första och vi ser att dessa värden även löser den andera. Vi har
alltså
där de två faktorerna är irreducibla i ![]() . Vi får alltså
en kropp
. Vi får alltså
en kropp ![]() genom att sätta
genom att sätta
![]() där
där
![]() . Då har
. Då har ![]() nollstället
nollstället ![]() i
i ![]() och vi kan faktorisera enligt faktorsatsen:
och vi kan faktorisera enligt faktorsatsen:
![]() .
.
Vi undersöker nu om ![]() har något nollställe i
har något nollställe i
![]() . Kvadratkomplettering ger
. Kvadratkomplettering ger
![]() . Vi
sätter
. Vi
sätter
![]() där
där
![]() och ska lösa
ekvationen
och ska lösa
ekvationen
![]() som
ger ekvationssytemet
som
ger ekvationssytemet
Den nedersta ekvationen ger ![]() eller
eller ![]() . Det första
alternativet ger
. Det första
alternativet ger ![]() i den första ekvationen, så att
i den första ekvationen, så att ![]() och
och ![]() . Vi får att
. Vi får att ![]() har nollställena
har nollställena
![]() .
Detta ger
.
Detta ger
Svar:
![]() där
där
![]() och
och
![]() i
i ![]() .
.
Enligt summeringsprincipen är
Handpåläggning ger
Vi får att
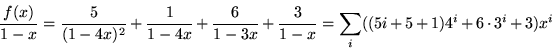
Vi har alltså att
För att bestämma perioden av ![]() ska vi bestämma det minsta
heltalet
ska vi bestämma det minsta
heltalet ![]() så att
så att
![]() är ett polynom. Vi har att
är ett polynom. Vi har att
![]() så
så
Eftersom ![]() är relativt prima med nämnaren ska vi bestämma
det minsta
är relativt prima med nämnaren ska vi bestämma
det minsta ![]() så att
så att ![]()
![]() och
och ![]() delar
delar ![]() .
.
Räknar vi modulo ![]() har vi
har vi ![]() så
så ![]() .
.
Räknar vi modulo ![]() har vi
har vi ![]()
![]() ,
,
![]() och
och
![]() så
så ![]() .
.
Gruppen
![]() har ordning
har ordning
![]() så ordningen av
så ordningen av ![]() delar
delar ![]() . Vi har
. Vi har
![]()
![]()
![]()
![]()
![]() och
och
![]() så
så
![]() .
.
Det minsta värdet på ![]() som uppfyller
som uppfyller ![]()
![]() och
och
![]() är
är ![]() . Perioden är alltså
. Perioden är alltså ![]() .
.
Svar:
![]() är periodisk med
period
är periodisk med
period ![]() .
.
- Gruppen
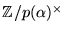 har ordning
har ordning 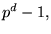 så för varje element
så för varje element 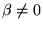 gäller att
gäller att
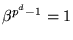 . Multiplicerar vi med
. Multiplicerar vi med 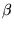 får vi att
får vi att
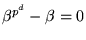 vilket även gäller för
vilket även gäller för
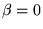 . Polynomet
. Polynomet 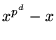 har alltså
har alltså 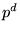 olika
nollställen i
olika
nollställen i
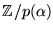 och är därför en produkt av
polynom av grad
och är därför en produkt av
polynom av grad 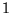 i
i
![$\mathbb{Z}/p(\alpha)[x]$](img137.png) . För att visa att
. För att visa att
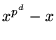 delar
delar 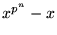 räcker det därför att inse att
alla element
räcker det därför att inse att
alla element 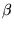 i
i
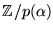 också är nollställen till
också är nollställen till
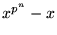 . Men eftersom
. Men eftersom 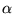 är nollställe till
är nollställe till 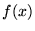 som
delar
som
delar 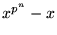 gäller att
gäller att
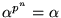 .
För
.
För
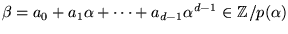 har vi därför att
har vi därför att
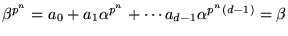 .
.
- Enligt divisionsalgoritmen har vi att
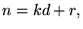 där
där
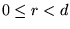 . Räknar vi modulo
. Räknar vi modulo 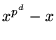 har vi enligt a)
har vi enligt a)
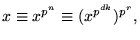 men också
men också
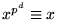 . Av det senare följer att
. Av det senare följer att
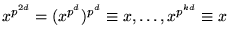 . Detta ger nu
. Detta ger nu
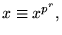 så att
så att 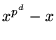 delar
delar
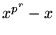 . Av gradskäl måste detta polynom vara 0, dvs
. Av gradskäl måste detta polynom vara 0, dvs
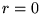 . Vi har därför att
. Vi har därför att 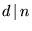 .
.