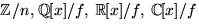Förslag till lösningar till MAN011 Aritmetik och
algebra, del 2, 00 04 17
- Radoperationer ger
Nollrummet består alltså av vektorer
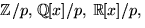 sådana att
sådana att
Lösningarna till detta är
där  och
och  kan väljas godtyckligt i
kan väljas godtyckligt i  .
Allmänna lösningen är alltså
.
Allmänna lösningen är alltså
Vektorerna
 och
och  genererar
alltså lösningsrummet. De är också linjärt oberoende ty den allmänna
lösningen blir
genererar
alltså lösningsrummet. De är också linjärt oberoende ty den allmänna
lösningen blir  bara är
bara är
 . De är därför
en bas för nollrummet till
. De är därför
en bas för nollrummet till  .
I den allmänna lösningen till ekvationssystemet
.
I den allmänna lösningen till ekvationssystemet
 kan vi välja
kan vi välja  och
och  goctyckligt i
goctyckligt i  och olika val ger olika lösningar. Antalet olika lösningar är därför
och olika val ger olika lösningar. Antalet olika lösningar är därför
 .
Svar:
.
Svar:
 och
och  samt
samt  .
.
- För att visa att
 är en kropp gäller det att visa att
är en kropp gäller det att visa att
 är irreducibelt i
är irreducibelt i ![$\mathbb{Q}[x]$](img20.gif) . Enligt
Eisensteins kriterium är detta fallet om det finns ett primtal som
delar
. Enligt
Eisensteins kriterium är detta fallet om det finns ett primtal som
delar  och
och  men vars kvadrat inte delar
men vars kvadrat inte delar  . Talet
. Talet  är
ett sådant primtal.
För att invertera
är
ett sådant primtal.
För att invertera  använder vi Euklides algoritm och får
använder vi Euklides algoritm och får
I  ger detta
ger detta
 eller
eller
 och alltså
och alltså
Svar:
 .
.
- Vi undersöker först om
 faktoriserar i
faktoriserar i
![$\mathbf Z/5[x]$](img30.gif) . En faktor
av grad
. En faktor
av grad  motsvarar ett nollställe i
motsvarar ett nollställe i  . Men
. Men
så faktorer av grad  saknas.
Vi undersöker om
saknas.
Vi undersöker om  har faktorer av grad
har faktorer av grad  genom att ansätta
genom att ansätta
 där
där  och
och
 . Identifiering av koefficienter ger ekvationssystemtet
. Identifiering av koefficienter ger ekvationssystemtet
Den nedersta ekvationen ger alternativen
 . Av symmeteriskäl behöver vi bara
undersöka de två försra alternativen. Det första ger
ekvationssystemet
. Av symmeteriskäl behöver vi bara
undersöka de två försra alternativen. Det första ger
ekvationssystemet
Första och tredje ekvavationen ger  vilket strider mot den andra
ekvationen.
Alternativet
vilket strider mot den andra
ekvationen.
Alternativet  ger i stället
ger i stället
Första och tredje ekvationenen ger  . Den första ger nu
. Den första ger nu  men
detta strider mot den andra ekvationen.
Eftersom
men
detta strider mot den andra ekvationen.
Eftersom  är av grad
är av grad  och saknar faktorer av så väl grad
och saknar faktorer av så väl grad  som
som
 , är
, är  irreducibelt.
Det betyder att
irreducibelt.
Det betyder att
![$K=\mathbb{Z}/5[x]/f(x)=\mathbb{Z}/5(\alpha)$](img46.gif) är en
kropp. I denna kropp har
är en
kropp. I denna kropp har  enligt en sats, nollställena
enligt en sats, nollställena
 och
och  som alla är olika.
Vi får alltså
som alla är olika.
Vi får alltså
Vi har
 vilket ger
vilket ger
Faktoriseringen av  i
i ![$K[x]$](img54.gif) blir alltså
blir alltså
Svar:
 där
där
 och
och
 .
.
- Vi skriver om
 och
och  med hjälp av
med hjälp av
 . Vi har
. Vi har
 och observerar att
och observerar att
Detta ger oss
Svar:
 .
.
- Eftersom
 är irreducibelt av grad
är irreducibelt av grad  är
är
 där
där
 en kropp med
en kropp med  element. De inverterbara elementen
i
element. De inverterbara elementen
i  bildar alltså en grupp med
bildar alltså en grupp med  element. Enligt Lagranges
sats gäller att
element. Enligt Lagranges
sats gäller att
 för alla inverterbara element i
för alla inverterbara element i  .
Detta ger att
.
Detta ger att  är en produkt av polynom av grad
är en produkt av polynom av grad  i
i
![$K[x]$](img54.gif) . Eftersom även
. Eftersom även  är en produkt av polynom av grad
är en produkt av polynom av grad  i
i
![$K[x]$](img54.gif) gäller att
gäller att
 i
i ![$K[x]$](img54.gif) .
Entydigheten i divisionsalgoritmen ger nu att
.
Entydigheten i divisionsalgoritmen ger nu att
 i
i
![$\mathbb{Z}/p[x]$](img75.gif) .
.
Jan-Alve Svensson
2000-04-26