- 2.
- (a)
- Vi har
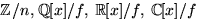 och
och 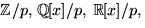 . Vi
ser att primtalet 17 delar samtliga koefficienter utan den
ledande i polynomet. Eftersom 172 inte delar
polynomets konstant är polynomet irreducibelt enligt Eisensteins kriterium.
. Vi
ser att primtalet 17 delar samtliga koefficienter utan den
ledande i polynomet. Eftersom 172 inte delar
polynomets konstant är polynomet irreducibelt enligt Eisensteins kriterium.
- 4.
- För att visa att
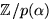 är en kropp ska vi visa att
p(x)=x4-3x+1 är irreducibelt i
är en kropp ska vi visa att
p(x)=x4-3x+1 är irreducibelt i ![$\mathbb Q[x]$](img4.gif) . Eftersom
polynomet har grad 4 räcker det att undersöka om det har delare av
grad 1 eller 2. En delare av grad 1 motsvarar ett rationellt
nollställe enligt faktorsatsen. De möjliga rationella nollställena
är
. Eftersom
polynomet har grad 4 räcker det att undersöka om det har delare av
grad 1 eller 2. En delare av grad 1 motsvarar ett rationellt
nollställe enligt faktorsatsen. De möjliga rationella nollställena
är  och inget duger, så p(x) saknar faktor av grad 1.
och inget duger, så p(x) saknar faktor av grad 1.
För att undersöka faktorer av grad 2 ansätter vi
p(x)=(x2+ax+b)(x2+cx+d), där vi kan förutsätta att
 och d är heltal, eftersom p(x) är primitivt, och att
och d är heltal, eftersom p(x) är primitivt, och att
 . Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet
. Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet

Den nedersta ekvationen ger möjligheterna b=d=1 och b=d=-1. Båda
alternativen ger att första och tredje ekvationerna strider mot
varandra. Lösning saknas. Därför saknar p(x) även delare av grad
2 och är därmed irreducibelt i ![$\mathbb Q[x]$](img9.gif) och
och  är en kropp.
är en kropp.
För att invertera använder vi Euklides algoritm på
 och
och  . Vi får
. Vi får

och vi får  .
. Svar:  .
.
- 5.
- Vi bestämmer egenenvärden till A genom att göra radoperationer på
 :
:


Egenvärdena är nollställena till  respektive
respektive
 d.v.s
d.v.s
 .
.
Vi bestämmer ett egenvärde hörande till vart och ett av dessa:

Vi ser att egenvektorer ges av (t.ex)  hörande till egenvärdena
hörande till egenvärdena  respektive 3,
respektive 3,
Sätter vi

har vi AC=CD. Eftersom kolonnerna i C hör till olika egenvärden
är de linjärt oberoende och C därmed inverterbar
Svar: 
- 6.
- Vi undersöker först om p(x) faktoriserar i
 . Eftersom
det är av grad 4 räcker det att undersök om det har en faktor av
grad 1 eller 2 i
. Eftersom
det är av grad 4 räcker det att undersök om det har en faktor av
grad 1 eller 2 i ![$\mathbb Z/5[x]$](img28.gif) . En faktor av grad 1
motsvarar ett nollställe i
. En faktor av grad 1
motsvarar ett nollställe i  enligt faktorsatsen. Vi har
enligt faktorsatsen. Vi har
 och
och  så p(x) saknar faktor av
grad 1.
så p(x) saknar faktor av
grad 1.
För att undersöka om p(x) har faktor av grad 2 ansätter vi
p(x)=(x2+ax+b)(x2+cx+d), där  . Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet
. Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet

Den översta ekvationen ger c=-a, som i den tredje ger 0=a(d-b)
med lösningarna a=0 eller b=d. Det första alternativet ger,
enligt andra ekvationen, b=2-d, som insatt i den sista ger
3=2d-d2, som saknar lösningar i  . Alternativet
b=d ger 3=b2 i sista ekvationen. Denna saknar lösning i
. Alternativet
b=d ger 3=b2 i sista ekvationen. Denna saknar lösning i
 . Därmed saknar p(x) även faktor av grad 2 i
. Därmed saknar p(x) även faktor av grad 2 i
![$\mathbb Z[5]$](img36.gif) och är därför irreducibelt.
och är därför irreducibelt.
Vi har därför kroppen  där
där
 där p(x) har
nollstället
där p(x) har
nollstället  men även
men även  .
.
Vi vet att p(x) även har nollstället
 så
faktorsatsen ger oss faktoriseringen
så
faktorsatsen ger oss faktoriseringen

Svar:  där
där
 och
och 
- 7.
- Vi ser att
 där
där  . Detta ger oss
f(x)=(1+2x)/(1-x2) och därmed
. Detta ger oss
f(x)=(1+2x)/(1-x2) och därmed



Svar:  .
.
- 8.
- Låt
 vara nollstället till
f(x)=a0+a1x+a2x2+a3x3.
vara nollstället till
f(x)=a0+a1x+a2x2+a3x3.
Vi har  och
och

Insättning av
nollstället ger att vi har

Vi ser att ekvationerna stämmer även om vi byter d mot -d, så
f(x) har nollställena  i L. Enligt faktorsatsen
kan vi faktorisera f(x) i L[x] enligt
i L. Enligt faktorsatsen
kan vi faktorisera f(x) i L[x] enligt

där ![$g(x)\in L[x]$](img58.gif) är av grad 1. Men
är av grad 1. Men ![$x^{2}-2cx+c^{2}-d^{2}a\in
K[x],$](img59.gif) delar f(x) i K[x] enligt divisionsalgoritmens
entydighet. Detta ger att
delar f(x) i K[x] enligt divisionsalgoritmens
entydighet. Detta ger att ![$g(x)\in K[x],$](img60.gif) d.v.s f(x) har, enligt
faktorsatsen, ett nollställe i K.
d.v.s f(x) har, enligt
faktorsatsen, ett nollställe i K.
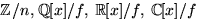 och
och 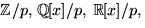 . Vi
ser att primtalet 17 delar samtliga koefficienter utan den
ledande i polynomet. Eftersom 172 inte delar
polynomets konstant är polynomet irreducibelt enligt Eisensteins kriterium.
. Vi
ser att primtalet 17 delar samtliga koefficienter utan den
ledande i polynomet. Eftersom 172 inte delar
polynomets konstant är polynomet irreducibelt enligt Eisensteins kriterium.
![]() och d är heltal, eftersom p(x) är primitivt, och att
och d är heltal, eftersom p(x) är primitivt, och att
![]() . Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet
. Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet

![]() och
och ![]() . Vi får
. Vi får
![]()
![]() .
.




![]() . Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet
. Identifiering av koefficienter ger att vi ska lösa
ekvationssystemet

![]() där
där
![]() där p(x) har
nollstället
där p(x) har
nollstället ![]() men även
men även ![]() .
.![]() så
faktorsatsen ger oss faktoriseringen
så
faktorsatsen ger oss faktoriseringen
![]()
![]()
![]()
![]()
![]() och
och
![]()
![]()
![]()