Lösning till tentamen i MAN011 Aritmetik och algebra,
del 2, 99 05 29.
- 1.
- Det gäller att visa att
![$p(x)=x^{3}+2x+4\in \mathbb Z/5[x]$](img1.gif) är
irreducibelt. Etftersom polynomet är av grad 3 räcker det, enligt
faktorsatsen, att kontrollera att det saknar nollställe i
är
irreducibelt. Etftersom polynomet är av grad 3 räcker det, enligt
faktorsatsen, att kontrollera att det saknar nollställe i
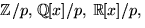 . Vi har p(0)=4, p(1)=2, p(2)=1, p(3)=p(-2)=2, p(4)=p(-1)=1.
Därmed är
. Vi har p(0)=4, p(1)=2, p(2)=1, p(3)=p(-2)=2, p(4)=p(-1)=1.
Därmed är 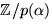 en kropp.
en kropp.
Vi bestämmer inversen med Euklides algoritm för en största gemensam
delare till polynomen  och
och
 och får
och får

Baklänges ger detta:

så
 i
i 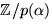 .
. - 2.
- Polynomet
![$x^4+3x^3+6x^2+3x+2 \in \mathbb Z/7[x]$](img9.gif) saknar linjärfaktorer, ty
p(0)=2, p(1)=1, p(2)=4, p(3)=3, p(-3)=5, p(-2)=3, p(-1)=3.
För att undersöka en eventuell faktor av grad 2 ansätter vi
p(x)=(x2+ax+b)(x2+cx+d), där a, b, c och d är i
saknar linjärfaktorer, ty
p(0)=2, p(1)=1, p(2)=4, p(3)=3, p(-3)=5, p(-2)=3, p(-1)=3.
För att undersöka en eventuell faktor av grad 2 ansätter vi
p(x)=(x2+ax+b)(x2+cx+d), där a, b, c och d är i  .
Identifiering av koefficienter ger ekvationssystemet
.
Identifiering av koefficienter ger ekvationssystemet

Den nedersta ekvationen ger (b,d)=(1,2), (3,3), (4,4) eller
(5,6). Fallen där b=d ger motstridiga första och tredje ekvationer.
Om (b,d)=(1,2) ger första och tredje ekvationer att a=0, c=3, men då
är andra ekvationen inte uppfyld. Slutligen ger (b,d)=(5,6) att
a=2 och c=1, så vi har faktoriseringen

Vi sätter  , där
, där  . Vi har
. Vi har  .Vi faktoriserar
.Vi faktoriserar  . Lösningen till
x2+x+6 är enligt formeln
. Lösningen till
x2+x+6 är enligt formeln  .
Vi faktoriserar
.
Vi faktoriserar  och därmed är
och därmed är

- 3.
- Att skriva vektorn som linjärkombination ger ett ekvationssystem
med utökad koefficientmatris:

Med radoperationer överför vi den till trappstegsform:

Vi konkluderar att vektorerna är linjärt oberoende över  ,men inte över
,men inte över  , och att
, och att

Likheten gäller fortfarande modulo 7.
- 4.
- Vi beräknar först egenvärdena till A:

och egenvärdena är rötterna till  .
.
En egenvektor till  är (1,1,1), till
är (1,1,1), till  (4,2,1)
och till
(4,2,1)
och till  (9,-3,1).
Vi har
(9,-3,1).
Vi har

Vi inverterar C:

Alltså är

och An=CDnC-1 blir

- 5.
- Monomer i utvecklingen har formen
 med
med  och all sådana förekommer. Svaret är alltså
antalet icke-negativa heltalslösningar till
och all sådana förekommer. Svaret är alltså
antalet icke-negativa heltalslösningar till
 , som är
, som är  .
.
![]()


![]()
![]()








![]()


![]()
![]()







