Förslag till lösning av Inlämningsuppgifter I

1.

Vi uppdelar först i $\mathbb Q[x]$ och faktoriserar därför nämnaren i $\mathbb Q[x]$ med hjälp av irreducibla polynom . Nämnaren f(x)=x⁴-3x³+x²+4 har de möjliga rationella nollställena $x=\pm 1,$ $\pm 2,$ $\pm 4$. Vi ser x=2 duger och f(x)=(x-2)(x³-x²-x-2). Vi ser att även x³-x²-x-2 har nollstället x=2. Vi får f(x)=(x-2)²(x²+x+1), där x²+x+1 är av grad 2 och saknar rationella nollställen och därmed är irreducibelt.

Vi ansätter nu uppdelningen till

$$\frac{5x^{2}+1}{(x-2)^{2}(x^{2}+x+1)}=\frac{A}{(x-2)^{2}}+\frac{B}{x-2} +\frac{Cx+D}{x^{2}+x+1}$$

Handpåläggning ger nu A=21/7=3. För att bestämma de övriga talen B, C och D, väljer vi några värden på x som är lätta att sätta in, t.ex. x=0, 1, respektive -1. Vi får då ekvationssystemet

$$\left\{\begin{array} {rcl} 1/4&=&3/4-B/2+D\\ 6/3&=&3-B+(C+D)/3\\ 6/9&=&1/3-B/3+(-C+D)/1\\ \end{array}\right.$$

som vi hyfsar till

$$\left\{\begin{array} {rcl} -1&=&-B+2D\\ -3&=&-3B+C+D\\ 1&=&-B-3C+3D\\ \end{array}\right.$$

Adderar vi den andra ekvationen multiplicerad med 3 till den nedersta får vi

$$\left\{\begin{array} {rcl} -1&=&-B+2D\\ -3&=&-3B+C+D\\ -8&=&-10B+6D\\ \end{array}\right.$$

Multiplicerar vi nu den översta ekvationen med -3 och adderar resultatet till den nedersta får vi -5=-7B, så B=5/7. Insatt i den översta ger detta D=-1/7, som sedan i den andra ekvationen ger C=-5/7. Vi har alltså

$$\frac{5x^{2}+1}{(x-2)^{2}(x^{2}+x+1)}=\frac{3}{(x-2)^{2}}+\frac{5/7}{x-2} -\frac{5x/7+1/7}{x^{2}+x+1}$$

i $\mathbb Q[x]$. Eftersom polynomet x²+x+1=(x-1/2)²+3/4 saknar reellt nollställe är det irreducibelt i $\mathbb R[x]$.

Svar:

$$\frac{5x^{2}+1}{(x-2)^{2}(x^{2}+x+1)}=\frac{3}{(x-2)^{2}}+\frac{5/7}{x-2} -\frac{5x/7+1/7}{x^{2}+x+1}$$

i båda fallen.

2.

För att visa att $\mathbb Q(\alpha),$ där $f(\alpha)=0$ är en kropp gäller det att visa att $f(x)\in \mathbb Q[x]$ är irreducibelt.

(a)

Väljer vi p=3 i Eisensteins kriterium ser vi att x⁵-6x+12 är irreducibelt, så $\mathbb Q(\alpha)$ är en kropp i detta fall.

(b)

Eftersom polynomet f(x)=x⁴+3x-1 har grad 4 gäller det att undersöka om det har en faktor av grad 1 eller 2.

En faktor av grad 1 motsvarar ett rationellt nollställe. De möjliga är $\pm 1,$ men inget duger. Faktor av grad 1 saknas. För att undersöka om polynomet har faktor av grad 2 ansätter vi f(x)=(x²+ax+b)(x²+cx+d), där vi kan anta att a, b, c och d är heltal eftersom polynomet är primitivt och att $b\leq d.$ Vi identifierar koefficienter och får ekvationssystemet

$$\left\{\begin{array} {rcl} 0&=&a+c\\ 0 &=& b+ac+d\\ 3&=& ad+bc\\ -1&=&bd \end{array}\right.$$

Den nedersta ekvationen ger b=-1 och d=1. Den andra ekvationen ger nu a=0 eller c=0. Båda alternativen ger motstridiga ekvationer i första och tredje raden. Ekvationssystemet saknar alltså lösning, så f(x) är irreducibelt och $\mathbb Q(\alpha)$ är en kropp även i detta fall.

(c)

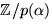Eftersom f(x)=x⁴+2x³-2x²+7x-2 är av grad 4 gäller det att undersöka om det har en faktor av grad 1 eller 2. En faktor av grad 1 motvarar ett rationellt nollställe. De möjlig är $\pm 1$ och $\pm 2,$ men inget duger. Polynomet saknar alltså faktorer av grad 2.

Det återstår att undersöka om polynomet har en faktor av grad 2. Vi ansätter därför f(x)=(x²+ax+b)(x²+cx+d), där vi kan förutsätta att a, b, c och d är heltal eftersom polynomet är primitivt och att $b\leq d$

Vi identifierar koefficienter och får ekvationssystemet

$$\left\{\begin{array} {rcl} 2&=&a+c\\ -2 &=& b+ac+d\\ 7&=& ad+bc\\ -2&=&bd \end{array}\right.$$

Den nedersta ekvationen ger b=-2 och d=1 eller b=-1 och d=2. Det första alternativet ger i tredje ekvationen 7=a-2c, som tillsammans med den översta ger c=-5/7, som inte är ett heltal.

Det andra alternativet ger i den tredje ekvationen 7=2a-c, som tillsammans med den första ger a=3 och c=-1. Vi ser att dessa värden på a, b, c och d löser ekvationssystemet. Polynomet f(x) är därför inte irreducibelt och $Q(\alpha)$ är därmed inte en kropp.

Svar: Ringen är en kropp i a) och b), men inte i c).

3.

För att undersöka om $g(x)\in \mathbb Q[x]/f(x)$ är irreducibelt gäller det (t.ex.) att undersöka om $\mbox{sgd}(g,f)=1$.

(a)

Vi ser att x²-2x+1=(x-1)² saknar irreducibel gemensam faktor med x³+1=(x+1)(x²-x+1), så elementet är inverterbart i detta fall. För att bestämma inversen använder vi Euklides algoritm baklänges och får först:

$$\begin{array} {rcl} x^{3}+1&=&(x+2)(x^{2}-2x+1)+3x-1\\ x^{2}-2x+1&=&(x/3-5/9)(3x-1)+4/9 \end{array}$$

Detta ger 4/9=(x²-2x+1)-(x/3-5/9)((x³+1)-(x+2)(x²-2x+1)), som i $\mathbb Q(\alpha)$ ger

$$4/9=(\alpha^{2}-2\alpha+1)(1+(\alpha/3-5/9)(\alpha+2))$$

eller $1=(\alpha^{2}-2\alpha+1)(-1/4+\alpha/4+3\alpha^{2}/4)$. Inversen är alltså $-1/4+\alpha/4+3\alpha^{2}/4$.

(b)

Vi ser att x⁴-2x+1 och x²-3x+2 har det gemensamma nollstället x=1, så x-1 delar deras största gemensamma delare som därför inte kan vara 1. Elementet är därför inte inverterbart.

Svar: Elementet är inverterbart bara i a). Inversen är i detta fall $-1/4+\alpha/4+3\alpha^{2}/4$.

4.

Eisensteins kriterium med p=3 ger att x²-3x+3 är irreducibelt i $\mathbb Q[x],$ så $\mathbb Q(\alpha),$ där $\alpha^{2}=3\alpha-3$ är en kropp. Vi har att $\mathbb Q(\alpha)=\{a+b\alpha\,\vert\,a,\,b\in \mathbb Q\}$.

Vi gör en kvadratkomplettering och får

$$x^{2}+(3-2\alpha)x+5-2\alpha=(x+(3-2\alpha)/2)^{2}+23/4-2\alpha.$$

Vi ansätter $x+(3-2\alpha)/2=a+b\alpha$ och ska lösa ekvationen $(a+b\alpha)^{2}= -23/4+2\alpha$. Vi utvecklar och använder att $\alpha^{2}=3\alpha-3$ och får då ekvationssystemet

$$\left\{\begin{array} {rcl} a^{2}-3b^{2}&=&-23/4\\ 2ab+3b^{2}&=&2 \end{array}\right.$$

För att få en ekvation med i ena ledet multiplicerar vi den nedre med 23/8 och lägger resultatet till den över. Vi får då 0=a²+23ab/4 +45b²/8. Kvadratkomplettering ger

0=a²+23ab/4 +45b²/8=(a+23b/8)²-169b²/64=(a-10b/8)(a+36b/8).

Av detta ser vi att a=-5b/4 eller a=-9b/2. Det första alternativet ger 2=2ab+3b²=b²/2, så $b=\pm 2$ och $a=\mp 5/2$. Det andra alternativet ger 2=-6b², som saknar rationell lösning.

Lösningarna är alltså

$$x=-(3-2\alpha)/2\pm (5/2-2\alpha)=\left\{\begin{array} {l} 1-\alpha\\ -4+3\alpha\end{array}\right.$$

Svar: Nollställena är $1-\alpha$ och $-4+3\alpha$.