Vi ansätter nu uppdelningen till
![]()
Handpåläggning ger nu A=21/7=3. För att bestämma de övriga talen B, C och D, väljer vi några värden på x som är lätta att sätta in, t.ex. x=0, 1, respektive -1. Vi får då ekvationssystemet
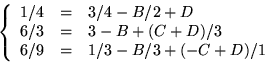
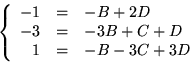
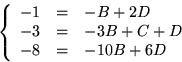
![]()
Svar:
![]()
- (a)
- Väljer vi p=3 i Eisensteins kriterium ser vi att x5-6x+12
är irreducibelt, så
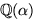 är en kropp i detta fall.
är en kropp i detta fall.
- (b)
- Eftersom polynomet f(x)=x4+3x-1 har grad 4 gäller det att
undersöka om det har en faktor av grad 1 eller 2.
En faktor av grad 1 motsvarar ett rationellt nollställe. De möjliga är
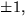 men inget duger. Faktor av grad 1 saknas. För att
undersöka om polynomet har faktor av grad 2 ansätter vi f(x)=(x2+ax+b)(x2+cx+d), där vi kan anta att a, b, c
och d är heltal eftersom polynomet är primitivt och att
men inget duger. Faktor av grad 1 saknas. För att
undersöka om polynomet har faktor av grad 2 ansätter vi f(x)=(x2+ax+b)(x2+cx+d), där vi kan anta att a, b, c
och d är heltal eftersom polynomet är primitivt och att 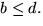 Vi identifierar koefficienter och får ekvationssystemet
Vi identifierar koefficienter och får ekvationssystemet
Den nedersta ekvationen ger b=-1 och d=1. Den andra ekvationen ger nu a=0 eller c=0. Båda alternativen ger motstridiga ekvationer i första och tredje raden. Ekvationssystemet saknar alltså lösning, så f(x) är irreducibelt och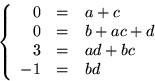
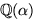 är en
kropp även i detta fall.
är en
kropp även i detta fall.
- (c)
- Eftersom f(x)=x4+2x3-2x2+7x-2 är av grad 4 gäller det
att undersöka om det har en faktor av grad 1 eller 2. En faktor
av grad 1 motvarar ett rationellt nollställe. De möjlig är
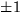 och
och 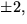 men inget duger. Polynomet saknar alltså faktorer av
grad 2.
men inget duger. Polynomet saknar alltså faktorer av
grad 2.
Det återstår att undersöka om polynomet har en faktor av grad 2. Vi ansätter därför f(x)=(x2+ax+b)(x2+cx+d), där vi kan förutsätta att a, b, c och d är heltal eftersom polynomet är primitivt och att
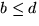
Vi identifierar koefficienter och får ekvationssystemet
Den nedersta ekvationen ger b=-2 och d=1 eller b=-1 och d=2. Det första alternativet ger i tredje ekvationen 7=a-2c, som tillsammans med den översta ger c=-5/7, som inte är ett heltal.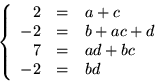
Det andra alternativet ger i den tredje ekvationen 7=2a-c, som tillsammans med den första ger a=3 och c=-1. Vi ser att dessa värden på a, b, c och d löser ekvationssystemet. Polynomet f(x) är därför inte irreducibelt och
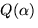 är därmed inte en
kropp.
är därmed inte en
kropp.
Svar: Ringen är en kropp i a) och b), men inte i c).
- (a)
- Vi ser att x2-2x+1=(x-1)2 saknar irreducibel gemensam
faktor med x3+1=(x+1)(x2-x+1), så elementet är inverterbart
i detta fall. För att bestämma inversen använder vi Euklides
algoritm baklänges och får först:
Detta ger 4/9=(x2-2x+1)-(x/3-5/9)((x3+1)-(x+2)(x2-2x+1)), som i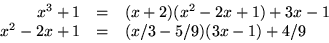
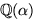 ger
ger
eller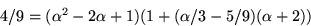
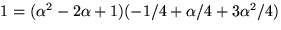 . Inversen är alltså
. Inversen är alltså 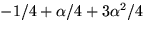 .
. - (b)
- Vi ser att x4-2x+1 och x2-3x+2 har det gemensamma
nollstället x=1, så x-1 delar deras största gemensamma delare
som därför inte kan vara 1. Elementet är därför inte
inverterbart.
Svar: Elementet är inverterbart bara i a). Inversen är i detta fall
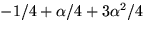 .
.
Vi gör en kvadratkomplettering och får
![]()
![]()
0=a2+23ab/4 +45b2/8=(a+23b/8)2-169b2/64=(a-10b/8)(a+36b/8).
Av detta ser vi att a=-5b/4 eller a=-9b/2. Det första alternativet ger 2=2ab+3b2=b2/2, såLösningarna är alltså
![]()
Svar: Nollställena är ![]() och
och ![]() .
.