- (a)
- Vi undersöker om f(x)=x4+4x3+2x2+3x+4 har någon
faktor av grad 1 genom att söka nollställe i
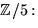 f(0)=4, f(1)=4, f(2)=1, f(3)=f(-2)=0. Enligt
faktorsatsen gäller att x-3=x+2 delar f(x):
f(0)=4, f(1)=4, f(2)=1, f(3)=f(-2)=0. Enligt
faktorsatsen gäller att x-3=x+2 delar f(x):
f(x)=(x+2)(x3+2x2+3x+2)
Vi undersöker om g(x)=x3+2x2+3x+2 har något nollställe i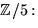 g(0)=2, g(1)=3, g(2)=4 g(3)=g(-2)=1 och
g(4)=g(-1)=0. Faktorsatsen ger att x-4=x+1 delar g(x):
g(0)=2, g(1)=3, g(2)=4 g(3)=g(-2)=1 och
g(4)=g(-1)=0. Faktorsatsen ger att x-4=x+1 delar g(x):
x3+2x2+3x+2=(x+1)(x2+x+2)
Vi undersöker om h(x)=x2+x+2 har något nollställe i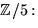 h(0)=0, h(1)=4, h(2)=3, h(3)=h(-2)=4 och
h(4)=h(-1)=2. Eftersom h(x) är av grad 2 och saknar nollställe
i
h(0)=0, h(1)=4, h(2)=3, h(3)=h(-2)=4 och
h(4)=h(-1)=2. Eftersom h(x) är av grad 2 och saknar nollställe
i 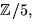 är det irreducibelt enligt faktorsatsen.
är det irreducibelt enligt faktorsatsen.
Polynomen x+2 och x+1 är irreducibla eftersom de är av grad 1.
Svar: f(x)=(x+2)(x+1)(x2+x+2).
- (b)
- Vi undersöker om f(x)=x4+x3+4x2+2x+4 har något
nollställe i
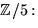 f(0)=0, f(1)=2, f(2)=3,
f(3)=f(-2)=4 och f(4)=f(-1)=1. Därmed saknar f(x) faktor av
grad 1. Vi undersöker om f(x) har faktor av grad 2 genom att
ansätta f(x)=(x2+ax+b)(x2+cx+d), där a, b, c och d
f(0)=0, f(1)=2, f(2)=3,
f(3)=f(-2)=4 och f(4)=f(-1)=1. Därmed saknar f(x) faktor av
grad 1. Vi undersöker om f(x) har faktor av grad 2 genom att
ansätta f(x)=(x2+ax+b)(x2+cx+d), där a, b, c och d 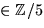 . Identifiering av koefficienter ger ekvationssystemet
. Identifiering av koefficienter ger ekvationssystemet
Den nedersta ekvationen ger b=1, d=4 eller b=2=d eller b=3=d (eller b=4, d=1).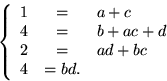
Alternativet b=1, d=4 ger 2=4a+c i tredje ekvationen. Subtraheras den första från detta får vi 1=3a, eller a=2. Där med är c=4 enligt den första ekvationen. Men nu stämmer inte den andra.
Alternativet b=d=2 ger ac=0 i den andra ekvationen, dvs a=0 eller c=0. Väljer vi a=0 blir c=1 enligt den första ekvationen. Med dessa värden på a, b, c och d stämmer samtliga ekvationer i systemet.
Vi har alltså
x4+x3+4x2+2x+4=(x2+2)(x2+x+2),
där de två polynomen av grad 2, enligt vad vi kontrollerat, saknar nollställen i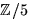 och därmed är irreducibla i
och därmed är irreducibla i ![$\mathbb Z/5[x]$](img6.gif) .
.Svar: x4+x3+4x2+2x+4=(x2+2)(x2+x+2).
För att invertera ![]() använder vi Euklides algoritm:
använder vi Euklides algoritm:
![]()
Svar: ![]() .
.
Vi ansätter f(x)=x4+2x3+4x2+4x+4=(x2+ax+b)(x2+cx+d), där
vi kan förutsätta att a, b, c och d är heltal, eftersom
polynomet är primitivt, och att ![]() . Vi får, genom att
identifiera koefficienter, ekvationssystemet
. Vi får, genom att
identifiera koefficienter, ekvationssystemet
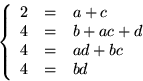
Första alternativet ger 4=a-4c i tredje ekvationen. Subtraheras
detta från den första får vi -2=5c, som saknar lösning
![]() .
.
Andra alternativet ger -2=a+c i tredje ekvationen vilket strider
mot den första. Tredje alternativet ger i stället 4=4a+c i den
tredje vilket, efter subtraktion med den första ger 2=3a som
saknar lösning ![]() .
.
Fjärde alternativet ger 0=ac i andra ekvationen, dvs a=0 eller c=0. Vi ser att a=0, b=d=2 och c=2 löser ekvationssystemet.
Vi har alltså
f(x)=(x2+2)(x2+2x+2),
där de två polynomen av grad 2 är irreducibla eftersom de saknar rationella nollställen, enligt vad vi kontrollerat.
Sätter vi nu ![]() där
där ![]() får vi
en kropp, där x2+2 har nollstället
får vi
en kropp, där x2+2 har nollstället ![]()
![]()
![]()
Vi har alltså kroppen ![]() där
där ![]() och
och
![]()
Svar: ![]() där
där ![]() och
och
![]() . I K[x] är
. I K[x] är
![]() .
.
Vi undersöker om f har faktor av grad 2 genom att ansätta
f(x)=(x2+ac+b)(x2+cx+d), där a, b, c och d ![]() . Identifiering av koefficienter ger ekvationssystemet
. Identifiering av koefficienter ger ekvationssystemet
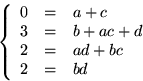
Alternativet b=1, d=2 ger 2=2a+c i tredje ekvationen. Tillsammans med den första ger detta a=2 och c=5. Men detta stämmer inte i den andra.
Alternativet b=3=d ger 3=a+c i den tredje vilket strider mot den första ekvationen.
Alternativet b=d=4 ger 4=a+c i den tredje vilket strider mot den första ekvationen.
Alternativet b=5, d=6 ger 2=6a+5c i den tredje vilket tillsammans med den första ger a=2 och c=5. Men detta stämmer inte i den andra ekvationen.
Polynomet f(x) saknar alltså även faktor av grad 2 och är därmed irreducibelt.
Sätter vi nu ![]() där
där ![]() så har
f(x) nollstället
så har
f(x) nollstället ![]() i K. Men
i K. Men
![]() så även
så även ![]() är nollställen
liksom
är nollställen
liksom ![]() och
och ![]() . Enligt en sats är alla
dessa olika. Vi får alltså
. Enligt en sats är alla
dessa olika. Vi får alltså
![]()
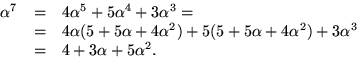
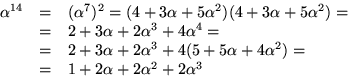
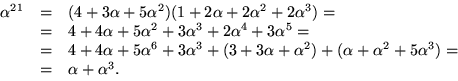
![]()
Svar: ![]() där
där
![]() och
och ![]() .
.