Förslag till lösning av Inlämningsuppgifter III

1.

Vi gör radoperationer på systemets koefficientmatris och får

$$\left( \begin{array} {rrrrr} 1&2&0&4&1\\ 2&0&2&3&1\\ 3&1... ...{rrrrr} 1&2&0&4&1\\ 0&1&2&0&4\\ 0&0&1&4&3\end{array}\right),$$

som är på trappstegsform. Ekvationssystemet är alltså ekvivalent med

$$\left\{ \begin{array} {rcrcrcrcrcl} x_{1}&+&2x_{2}&+& & &4... ...{5}&=&0\\ & & & &x_{3}&+&4x_{4}&+&3x_{5}&=&0\end{array}\right.$$

Löser vi detta nerifrån och upp får vi

$$\begin{array} {rcl} x_{3}&=&x_{4}+2x_{5}\\ x_{2}&=&3x_{3}+... ...&3x_{2}+x_{4}+4x_{5}=3(3x_{4}+2x_{5})+x_{4}+4x_{5}=0\end{array}$$

Den allmänna lösningen är alltså

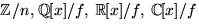
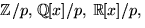
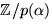
(x₁,x₂,x₃,x₃,x₄,x₅)= (0,3x₄ +2x₅,x₄+2x₅,x₄,x₅)=x₄(0,3,1,1,0)+x₅(0,2,2,0,1),

där x₄ och x₅ är godtyckliga i $\mathbb Z/5$. Olika val av x₄ och x₅ ger lösningar med olika koordinater på plats 4 och 5, så antalet lösningar är $5\cdot 5=25$.Vi ser att lösningsrummet genereras av $\mathbf v_{1}=(0,3,1,1,0)$ och v₂=(0,2,2,0,1). De är också linjärt oberoende för vi får lösningen $\mathbf 0$ bara om x₄=x₅=0.

Svar: T.ex. (0,3,1,1,0) och (0,2,2,0,1). Antalet lösningar är 25.

2.

Vi gör radoperationer på (A|I) till (A'|I') på reducerad trappstegsform. Om A'=I, så är A inverterbar med inversen I'.

$$\left( \begin{array} {rrr\vert rrr} 1&2&1&1&0&0\\ 3&4&1&0... ... 0&1&1&5&3&0\\ 0&1&3&3&0&2\\ \end{array}\right)\rightarrow$$

$$\left( \begin{array} {rrr\vert rrr} 1&2&1&1&0&0\\ 0&1&1&5... ... 0&1&0&6&1&6\\ 0&0&1&6&2&1\\ \end{array}\right)\rightarrow$$

$$\left( \begin{array} {rrr\vert rrr} 1&0&0&4&3&1\\ 0&1&0&6&1&6\\ 0&0&1&6&2&1\\ \end{array}\right)$$

Vi löser ekvationen AXA^-1=B genom att först multiplicera båda sidor med A^-1 från vänster. Vi får då XA^-1=A^-1B. Multiplicerar vi sedan med A från höger får vi X=A^-1BA:

$$X=\left( \begin{array} {rrr} 4&3&1\\ 6&1&6\\ 6&2&1 \end... ...begin{array} {rrr} 2&6&1\\ 4&4&6\\ 6&1&1 \end{array}\right)$$

3.

Vi bestämmer först matrisens egenvärden; vi ska bestämma för vilka $\lambda$ som $A-\lambda I$ inte är inverterbar. Radoperationer ger

$$\left( \begin{array} {rrr} -\lambda&1&2\\ 2&1-\lambda&1\\... ...2\lambda&2+2\lambda-\lambda^{2} \end{array}\right)\rightarrow$$

$$\left( \begin{array} {rrr} 1&2&2-\lambda \\ 0&1&2-\lambda... ...^{2}-(1+2\lambda)(2-\lambda^{2}) \end{array}\right)\rightarrow$$

Vi ser att rangen är <3 precis när $0=2+2\lambda-\lambda^{2}-(1+2\lambda)(2-\lambda^{2})= 2\lambda^{3}+\lambda=2\lambda(\lambda^{2}+2)=2\lambda(\lambda-1)(\lambda-2)$.Egenvärdena är alltså $\lambda_{1}=0,$ $\lambda_{2}=1$ och $\lambda_{3}=2$.

Vi bestämmer en egenvektor $\mathbf v_{1}$ hörande $\lambda_{1}$. Vi ska ha $(A-\lambda_{1}I)\mathbf v_{1}=\mathbf 0$. Radoperationerna ovan ger

$$A-0I\rightarrow \left( \begin{array} {rrr} 1&2&2\\ 0&1&2\\ 0&0&0 \end{array}\right),$$

så $\mathbf v_{1}=(2,1,1)$ duger. Vi gör på samma sätt med $\lambda_{2}=1$ och $\lambda_{3}=2$. Radoperationer ger

$$A-I\rightarrow\left( \begin{array} {rrr} 1&2&1\\ 0&1&1\\ ... ...egin{array} {rrr} 1&2&0\\ 0&1&1\\ 0&0&0 \end{array}\right),$$

så vi ser att $\mathbf v_{2}=(1,2,1)$ respektive $\mathbf v_{3}=(2,2,1)$.Sätter vi nu

$$C=\left( \begin{array} {rrr} \mathbf v_{1}&\mathbf v_{2}&\... ...egin{array} {rrr} 0&0&0\\ 0&1&0\\ 0&0&1 \end{array}\right),$$

så har vi AC=CD. Eftersom egenvektorerna hör till olika egenvärden är C inverterbar.

Svar:

$$C=\left( \begin{array} {rrr} \mathbf v_{1}&\mathbf v_{2}&\... ...egin{array} {rrr} 0&0&0\\ 0&1&0\\ 0&0&1 \end{array}\right),$$

4.

Vi har $u(x)^{2}=\sum_{i}(i+1)x^{i},$ där $u(x)=\sum_{i}x^{i}=1/(1-x),$ så $\sum_{i}(1+i)x^{i}/(-2)^{i}=u(-x/2)^{2}$.

Multiplicerar vi u(-x/2)²=1/(1+x/2)² med u(x)=1/(1-x) får vi en ny potensserie vars koefficient framför xⁿ är $\sum_{i=0}^{n}(1+i)/(-2)^{i},$ enligt summeringsprincipen. Partialbråksuppdelning ger ansatsen

$$\frac{1}{(1-x)(1+x/2)^{2}}=\frac{A}{1-x}+\frac{B}{(1+x/2)^{2}}+\frac{C}{1+x/2}.$$

Handpåläggning ger A=4/9 och B=1/3. Insättning av x=0 (t.ex.) ger nu 1=4/9+1/3+C, så C=2/9.

Detta ger oss att

$$\begin{array} {rcl} u(x)u(x/2)^{2}&=&4u(x)/9+u(x/2)^{2}/3+2u... ...i}(i+1)x^{i}/(3(-2)^{i})+\sum_{i}2x^{i}/(9(-2)^{i}).\end{array}$$

Koefficienten framför xⁿ blir alltså 4+(n+1)/(3(-2)ⁿ)-10/(3(2ⁿ)), så

$$\sum_{i=0}^{n}(1+i)/2^{i}=\frac{4}{9}+\frac{3n+5}{9(-2)^{n}}$$

Svar: $\sum_{i=0}^{n}(1+i)/2^{i}=4/9+(3n+5)/(9(-2)^{n})$.