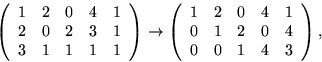
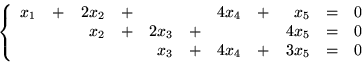
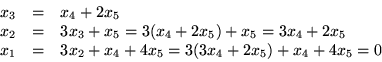
(x1,x2,x3,x3,x4,x5)= (0,3x4 +2x5,x4+2x5,x4,x5)=x4(0,3,1,1,0)+x5(0,2,2,0,1),
där x4 och x5 är godtyckliga iSvar: T.ex. (0,3,1,1,0) och (0,2,2,0,1). Antalet lösningar är 25.
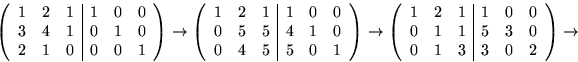
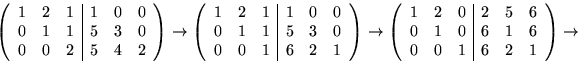
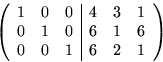
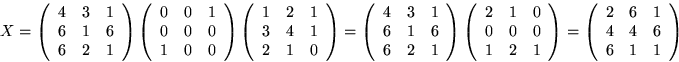
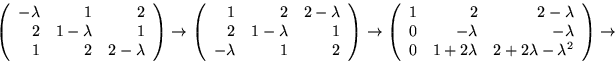
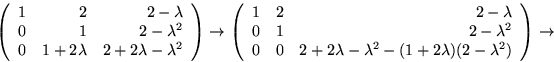
Vi bestämmer en egenvektor ![]() hörande
hörande ![]() . Vi
ska ha
. Vi
ska ha ![]() . Radoperationerna
ovan ger
. Radoperationerna
ovan ger
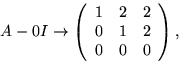
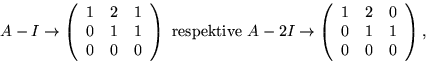
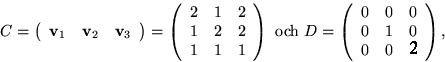
Svar:
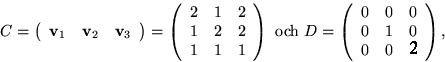
Multiplicerar vi u(-x/2)2=1/(1+x/2)2 med u(x)=1/(1-x) får vi en ny
potensserie vars koefficient framför xn är
![]() enligt
summeringsprincipen. Partialbråksuppdelning ger ansatsen
enligt
summeringsprincipen. Partialbråksuppdelning ger ansatsen
![]()
Detta ger oss att
![]()
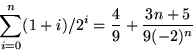
Svar: ![]() .
.