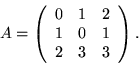
Beräkna
Låt ![]() vara ett primtal och
vara ett primtal och ![]() en irreducibel delare till
en irreducibel delare till
![]() av grad
av grad ![]() i
i
![]() .
.
- Visa att
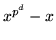 delar
delar 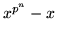 i
i
![$\mathbb{Z}/p[x],$](img27.png) t.ex. genom att
studera de båda polynomens nollställen i kroppen
t.ex. genom att
studera de båda polynomens nollställen i kroppen
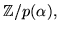 där
där 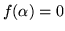 .
. - Visa att
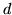 delar
delar 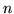 .
.
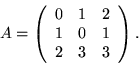
Låt ![]() vara ett primtal och
vara ett primtal och ![]() en irreducibel delare till
en irreducibel delare till
![]() av grad
av grad ![]() i
i
![]() .
.
Efter skrivningstidens slut finns förslag till lösningar på kursens hemsida :
http://www.math.chalmers.se/Math/Grundutb/GU/MAN011/H99-2
Skrivningen beräknas vara färdigrättad fredagen den 28 januari. I så fall kan de återfås på mottagningen i Matematiskt centrum samma dag. Öppettider är måndag - fredag kl 12.30-13.00. Vardagar efter kl 14.00 kan man få reda på resultat på telefon 7723509.