Tentamen i MAN011 Aritmetik och algebra, del 2, 5p,
00 04 17, kl 8.45-13.45.
- Låt
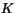 vara en kropp. Visa att varje polynom av grad
vara en kropp. Visa att varje polynom av grad 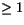 i
i
![$K[x]$](img5.gif) kan skrivas som en produkt av irreducibla polynom.
kan skrivas som en produkt av irreducibla polynom.
- Låt
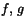 och
och  vara polynom med rationella koefficienter, sådana
att
vara polynom med rationella koefficienter, sådana
att 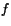 och
och 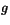 är relativt prima samt
är relativt prima samt
 .
Visa att det finns polynom
.
Visa att det finns polynom
![$a,\,b\in \mathbb{Q}[x],$](img11.gif) så att
så att
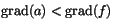 eller
eller 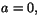
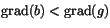 eller
eller 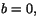 samt
samt
- Visa att om vektorerna
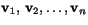 hör till olika egenvärden till matrisen
hör till olika egenvärden till matrisen 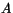 med
element i kroppen
med
element i kroppen 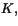 så är de linjärt oberoende.
så är de linjärt oberoende.
- Bestäm en bas för nollrummet till matrisen
som har element i 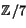 .
Hur många olika lösningar har ekvationssystemet
.
Hur många olika lösningar har ekvationssystemet
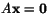 ?
?
- Visa att
![$K=\mathbb{Q}[x]/p(x),$](img23.gif) där
där
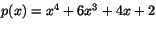 är en kropp
och bestäm inversen till
är en kropp
och bestäm inversen till 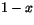 i
i 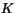 .
.
- Låt
![$f(x)=x^4+3x^3+2x^2+3x+2\in \mathbb{Z}/5[x]$](img26.gif) . Bestäm en så liten
kropp
. Bestäm en så liten
kropp 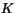 som möjligt, så att
som möjligt, så att 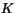 innehåller
innehåller 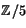 och
och 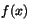 är en produkt av polynom av grad
är en produkt av polynom av grad 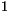 i
i ![$K[x]$](img5.gif) . Ange faktoriseringen!
. Ange faktoriseringen!
- Låt
vara formella potensserier i
![$\mathbb{Z}/3[[x]]$](img31.gif) . Bestäm deras produkt.
. Bestäm deras produkt.
- Antag att
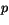 är ett primtal och
är ett primtal och
![$q(x)\in \mathbb{Z}/p[x]$](img33.gif) ett
irreducibelt polynom av grad
ett
irreducibelt polynom av grad 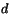 , Visa att
, Visa att
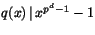 (i
(i
![$\mathbb{Z}/p[x]$](img36.gif) ).
).