Tentamen i MAN011 Aritmetik och algebra, del 2,
99 05 29, kl 8.45-13.45.
- 1.
- (a)
- Låt K vara en kropp. Vad menas med att vektorerna
v1, ..., vn i Km är linjärt oberoende?
- (b)
- Låt A vara en
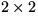 matris med element i kroppen K
med två skilda egenvärden
matris med element i kroppen K
med två skilda egenvärden 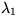 ,
, 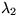 . Visa att om v1 och v2 är egenvektorer till respektive
. Visa att om v1 och v2 är egenvektorer till respektive 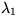 och
och
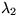 , så är de linjärt oberoende.
, så är de linjärt oberoende.
- 2.
- Formulera och bevisa faktorsatsen för polynom i K[x], där K
är en kropp.
- 3.
- Låt f vara ett polynom i K[x], där K är en kropp. Visa att
![$g\in K[x]/f$](img4.gif) är
inverterbart om och endast om
är
inverterbart om och endast om 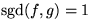 .
. - 4.
- Visa att
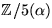 , där
, där 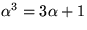 , är en kropp och invertera elementet
, är en kropp och invertera elementet
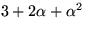 .
. - 5.
- Bestäm en så liten kropp K som möjligt, som innehåller
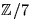 ,
sådan att polynomet
,
sådan att polynomet
![$x^4+3x^3+6x^2+3x+2 \in \mathbb Z/7[x]$](img10.gif) faktoriserar som
en produkt av polynom av grad
1 i K[x] och ange denna.
faktoriserar som
en produkt av polynom av grad
1 i K[x] och ange denna.
- 6.
- (a)
- Avgör om vektorerna
(1,2,3,4), (1,-2,3,-4) och
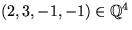 är linjärt beroende. Skriv vektorn (1,9,-4,11) som linjärkombination
av de tre givna.
är linjärt beroende. Skriv vektorn (1,9,-4,11) som linjärkombination
av de tre givna.
- (b)
- Samma frågor om element uppfattas som tal i
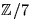 .
.
- 7.
- Matrisen
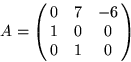
har element i 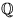 . Bestäm en inverterbar matris C och en
diagonal matris D, så att A=CDC-1.
Beräkna An for alla
. Bestäm en inverterbar matris C och en
diagonal matris D, så att A=CDC-1.
Beräkna An for alla 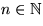 .
. - 8.
- Hur många termer får man då man utvecklar
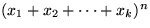 ?
?
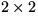 matris med element i kroppen K
med två skilda egenvärden
matris med element i kroppen K
med två skilda egenvärden 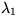 ,
, 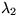 . Visa att om v1 och v2 är egenvektorer till respektive
. Visa att om v1 och v2 är egenvektorer till respektive 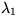 och
och
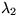 , så är de linjärt oberoende.
, så är de linjärt oberoende.
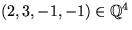 är linjärt beroende. Skriv vektorn (1,9,-4,11) som linjärkombination
av de tre givna.
är linjärt beroende. Skriv vektorn (1,9,-4,11) som linjärkombination
av de tre givna.
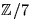 .
.