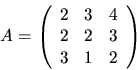Tentamen i MAN011 Aritmetik och algebra, del 2,
99 04 10, kl 8.45-13.45.
- 1.
- Formulera och bevisa faktorsatsen för polynom i K[x], där K
är en kropp.
- 2.
- (a)
- Formulera och bevisa Eisensteins kriterium för ett primitivt
polynom.
- (b)
- Är p(x)=x12+34x4+51x3-221 irreducibelt i
![$\mathbb Q[x]$](img1.gif) ?
?
- 3.
- Antag att
![$g,h\in \mathbb Q[x]$](img2.gif) är relativt prima och att
är relativt prima och att ![$f\in
\mathbb Q[x]$](img3.gif) har lägre grad än gh. Visa att det finns polynom
har lägre grad än gh. Visa att det finns polynom
![$a,b\in \mathbb Q[x],$](img4.gif) så att
så att
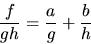
där a och b är eller har lägre grad än g respektive h.
- 4.
- Visa att
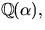 där
där 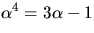 är en kropp och
bestäm inversen till
är en kropp och
bestäm inversen till 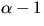 i
i 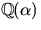 .
. - 5.
- Bestäm, om möjligt, en diagonal matris D och en inverterar matris
C, så att A=CDC-1, där A är matrisen
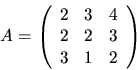
med element i 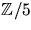 .
. - 6.
- Ange en så liten kropp K som möjligt, som innehåller
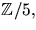 så att p(x) = x4+2x2+3 faktoriserar som en produkt av polynom av
grad 1 i K[x]. Bestäm faktoriseringen.
så att p(x) = x4+2x2+3 faktoriserar som en produkt av polynom av
grad 1 i K[x]. Bestäm faktoriseringen.
- 7.
- Bestäm inversen till den formella potensserien
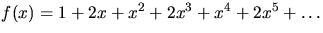 i
i ![$\mathbb Z/7[[x]]$](img14.gif) .
. - 8.
- Antag att K är en kropp och att
![$x^{2}-a\in K[x]$](img15.gif) är
irreducibelt. Visa att om
är
irreducibelt. Visa att om ![$f(x)\in K[x]$](img16.gif) är ett polynom av grad 3
som har ett nollställe i
är ett polynom av grad 3
som har ett nollställe i 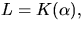 där
där 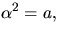 så har det
ett nollställe i K.
så har det
ett nollställe i K.
Efter skrivningstidens slut finns förslag till lösningar på
http://www.math.chalmers.se/Math/Grundutb/GU/MAN011/H98-2/
Skrivningen beräknas vara färdigrättad fredagen den 16 april. Rättade
skrivningar återfås på mottagningen för matematik i matematiskt
centrum. Mottagningen är öppen måndag till fredag 12.30-13.00.
![$\mathbb Q[x]$](img1.gif) ?
?
![]()
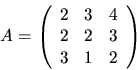
![]()